Equation 1
This equation will enable you to calculate the Relative Humidity in equilibrium with a salt solution. You will need to provide the concentration in Mol, the ionisation state of the salt (how many species it dissociates into) and a term describing the the specific volume of the solute (for sodium chloride y = 0.027, for ammonium sulfate y = 0.074, for sodium acetate y = 0.054, for sodium malonate y = 0.095, for magnesium sulphate y = 0.045, for Monopotassium phosphate y = 0.058 and for Dipotassium phosphate y = 0.071). Raoult's law breaks down for lithium chloride (y=0.023) concentrations over 2.5M with RH values much lower than predicted.
The Relative Humidity (RH) in equilibrium with solutions can be understood in terms of Raoult's law. It has two aspects that are counter-intuitive and lead to some surprising observations. The first is that the number of equivalent molecules in solution must be accounted for. This means that for sodium chloride, each ion in solution counts as a molecular equivalent. This requires knowledge of the ionization behaviour of the substance in solution. For example, ammonium sulfate effectively dissociates into two ions [NH4+ and (NH4SO4)-] and not three as might be expected. Raoult's law starts to break down for PEG solutions over a molecular weight of 1000 Da but this can be corrected using the Flory-Huggins model for the entropy of mixing (used in equation 2).
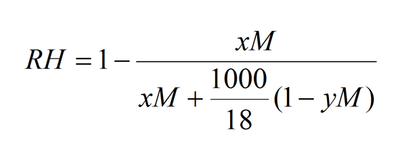
The parameter y can be calculated from this equation: y= (1/ρ)m/1000, where ρ is the density of the salt and m is the molecular weight.
partners
European Synchrotron Radiation Facility - 71, avenue des Martyrs, CS 40220, 38043 Grenoble Cedex 9, France.