- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2001
- Magnetism and Electronic Properties of Solid
- X-ray Magnetochiral Dichroism: A New Probe for Parity-violating Magnetic Solids
X-ray Magnetochiral Dichroism: A New Probe for Parity-violating Magnetic Solids
Natural Optical Activity (OA) of visible light was discovered early in the 19th century. In contrast, natural OA of X-rays was discovered quite recently [1]. Unlike magneto-optical spectroscopies, e.g. Faraday rotation, Magnetic Circular or linear dichroisms (MCD,MLD), which are all consistent with the usual electric dipole approximation, OA mixes multipole moments of opposite parity and thus requires odd space parity. Typically, OA of X-rays is caused by electric dipole-electric quadrupole E1.E2 interference terms [1]. It has long been argued that OA effects could be either even or odd with respect to time-reversal: time-reversal even OA properties are called natural whereas time-reversal odd properties are called non-reciprocal. A non-reciprocal X-ray magnetic linear dichroism (nr-XMLD) has recently been measured at the ESRF [2]. We report below another non-reciprocal effect in the X-ray range which we called X-ray Magnetochiral Dichroism (XMD). We stress that XM
D, unlike X-ray magnetic circular dichroism (XMCD), does not require a polarised beam since it is a property of the Stokes component S0.
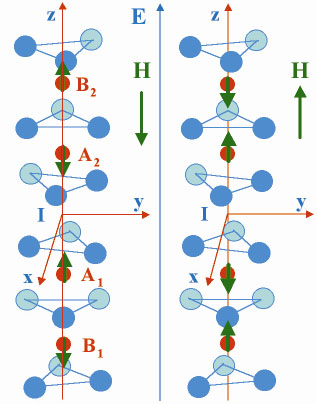 |
Fig. 105: Magnetic structure of the two 180° domains grown by magnetoannealing. |
Magnetoelectric (ME) solids are good candidates to detect XMD since magnetoelectric properties are odd with respect to Parity (P) and time reversal (Q) but are invariant in the product P
. The generic example of ME crystals is Cr2O3: it has the centrosymmetric corundum space group (R
c) but it belongs to the non-centrosymmetric
'm' space-time group below the Néel temperature. The spin moments can order in either one of the two 180° domains shown in Figure 105. One can grow such single domains by magnetoelectric annealing: it consists in heating the crystal in the paramagnetic phase and in applying simultaneously along the c axis a modest electric field E (5 kV/cm) plus a weak magnetic field H (± 0.5T). XM
D experiments were carried out at the ESRF beamline ID12, all spectra being recorded in the fluorescence excitation mode using the most convenient backscattering configuration. We produced artificially unpolarised light by incoherent superposition of fluorescence excitation spectra recorded with right and left circularly polarised incident photons: F0 = F[Rcp] + F[Lcp]. We have reproduced in Figure 106 the XM
D spectrum measured at T = 50K of a (001) Cr2O3 single crystal with the c axis parallel to the wavevector k. It is shown that the signal can be as large as 1.6% due to the strong contribution of the E1E2 interference terms in the X-ray regime. It also appears from Figure 106 that the same XM
D spectrum can be obtained using a powdered pellet of Cr2O3: the price to be paid is, however, a reduction (1:6) of the amplitude of the signal whereas the theory of XM
D predicts a slightly smaller reduction (1:5). Whereas X-ray natural circular dichroism (XNCD) can only be detected in single crystals, it is quite remarkable that XM
D can be measured in a powder due to the fact that the orientational isotropy is broken by the ME order.
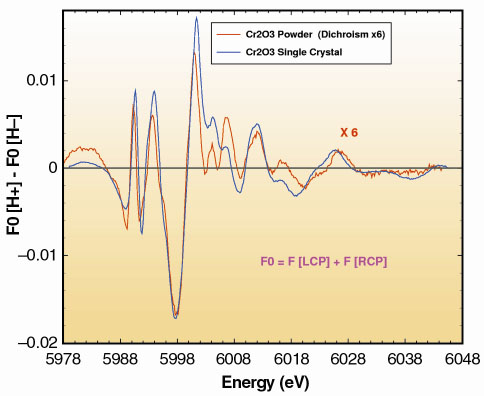 |
Fig. 106: Comparison of the XM |
At this stage, there is no existing ab initio computer program which would allow the proper simulation of the XMD spectra but, nevertheless, some valuable information can yet be extracted from the edge selective OA sum rules derived recently by Carra and co-workers. The effective operator
z which describes the mixing in the ground state of p and d atomic orbitals at the Cr absorbing site was identified with the orbital anapole. According to group theory, the universally cited magnetic group
'm' of Cr2O3 is not compatible with an invariant anapole moment. There is, however, no deep contradiction with our experiment: our XM
D spectra reveal that this magnetic group may be suitable to describe the spin configuration but not the overall magnetic symmetry including orbital moments and currents. In other words, the spin anapole moment of Cr2O3 certainly vanishes but it is our interpretation that the true space-time symmetry is most probably only
' since this group admits the orbital anapole moment
z as invariant.
References:
[1] J. Goulon, C. Goulon-Ginet, A. Rogalev, V. Gotte, C. Malgrange, Ch . Brouder and C.R. Natoli, J. Chem. Phys. 108, 6394-6403 (1998).
[2] J. Goulon, A. Rogalev, C. Goulon-Ginet, G. Benayoun, L. Paolasini, Ch. Brouder, C. Malgrange and P.A. Metcalf, Physical Review Letters, 85, 4385-8 (2000).
Principal Publication and Authors:
J. Goulon (a), A. Rogalev (a), F. Wilhelm (a), C. Goulon-Ginet (a,b), P. Carra (a), D. Cabaret (c) and Ch. Brouder (c), submitted to Physical Review Letter (2002).
(a) ESRF
(b) Université J. Fourier Grenoble-I, Faculté de Pharmacie, La Tronche (France)
(c) Universités Paris VI-VII, Laboratoire de Minéralogie-Cristallographie associé au CNRS, Paris (France)



