- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- Enabling Technologies
- Graphic cards on supercomputers for high performance electronic structure calculations
Graphic cards on supercomputers for high performance electronic structure calculations
Quantum mechanics and electromagnetism are widely perceived as leading to a “first-principles” approach to materials and nanosystems: if the needed software applications and corresponding hardware were available, their properties could be obtained without any adjustable parameters (nuclei characteristics being given). Still, such “first-principles” equations (e.g. N-body Schrödinger equation) are too complex to be handled directly. Fundamental quantities cannot be represented faithfully for N bigger than about a dozen on the computing hardware that is available today.
The Density-Functional Theory (DFT), in its Kohn-Sham single particle approach, is at present the most widely used methodology to address this problem. The complexity of the “first-principles” approach can be significantly reduced at the expense of some approximations. On the basis of such methodologies, in the eighties, it became clear that numerous properties of materials, like total energies, electronic structure, and dynamical, dielectric, mechanical, magnetic, vibrational properties, can be obtained with an accuracy that can be considered as truly predictive.
The physical properties which can be analysed via such methods are tightly connected to the computational power which can be exploited for calculation. A high-performance computing (HPC) DFT program will make the analysis of more complex systems and environments possible, thus opening a path towards new discoveries.
The deployment of massively parallel supercomputers in the last decade has opened new paths toward the exploitation of the computational power, by changing the programming paradigms in view of improved efficiency. In other words, the more computing power is available combined with code parallelisation, the better the predictions from a DFT program.
Another point is the nature of the basis set to expand the wavefunctions of the systems. The range of applications of a DFT program is tightly connected to the properties of the basis set. Non-localised basis sets like plane waves are highly suitable for periodic and homogeneous systems. Localised basis sets, like Gaussians, can achieve moderate accuracy with small numbers of degrees of freedom, but are in turn non-systematic, which may lead to over completeness and numerical instabilities before convergence is reached.
Daubechies wavelets have virtually all the properties which one might desire in view of DFT calculations. They are both orthogonal and systematic (like plane waves), and also localised (like Gaussians). In addition, they have some other properties (multi-resolution, adaptivity) thanks to which the computational operations can be expressed analytically.
BigDFT is a European project which started in 2005. Grouping four European laboratories, its aim was to build a new DFT program from scratch, based on Daubechies wavelets, and conceived to run on massively parallel architectures.
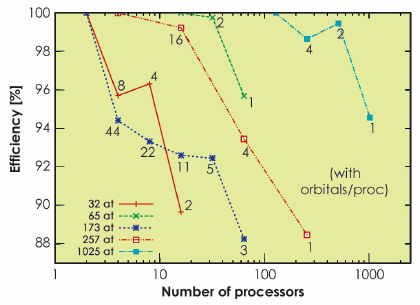
At the end of the project, in 2008, the first stable version of the BigDFT code was distributed under the GNU-GPL license, thus freely available for everyone [1]. This version was robust, and showed very good performances and excellent efficiency (about 95%, see Figure 156) for parallel and massively parallel calculations. Following this, the BigDFT code started to be used by different laboratories for high performance DFT calculations.
 |
|
Fig. 156: Efficiency of the parallel implementation of the software for several runs with different numbers of atoms. Excellent performance (around 95%) was recorded. |
Recently, new emerging architectures have shown their potential for high-performance computing. The Graphics Processing Units (GPU), intitially used by the computer gaming community, can be used for general purpose calculations, among which research applications. This gives rise to the so-called “hybrid” architectures, in which several CPUs can be combined with one or more GPU, in order to further increase the computational power. The porting of different sections of the BigDFT code to run on the GPU was then performed. The first hybrid version of the code was prepared in April 2009.
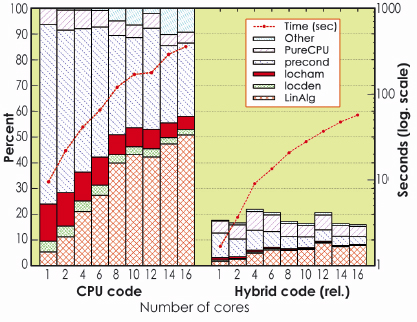
The GPU-based acceleration fully preserves the efficiency of the code. In particular, the code is able to run on many cores which may or may not have a GPU associated, and thus on parallel and massively parallel hybrid machines. Considerable increases in execution speed can be achieved, between a factor of 20 for some operations and a factor of 6 for the whole DFT code (see Figure 157). Such results can however be further improved by optimising the present GPU routines, and by accelerating other sections of the code.
 |
|
Fig. 157: Relative speed increase for the hybrid BigDFT program with respect to the equivalent CPU-only run, as a function of the number of CPU cores. A speed increase of a factor of around 6 with the hybrid CPU-GPU architecture, in double precision computation can be obtained, without altering parallel efficiency. |
For the first time, a systematic electronic structure code has been able to run on hybrid (super)computers in massively parallel environments [2]. These results open a path towards the use of hybrid architectures for electronic structure calculations. Unprecedented performance can be obtained for the prediction of new material properties.
For these results, the Bull-Joseph Fourier Prize 2009 was awarded to Luigi Genovese of the ESRF Theory Group.
References
1] L. Genovese, A. Neelov, S. Goedecker, T. Deutsch, S.A. Ghasemi, A. Willand, D. Caliste, O. Zilberberg, M. Rayson, A. Bergman and R. Schneider, J. Chem. Phys. 129, 014109 (2008).
[2] L. Genovese, M. Ospici, T. Deutsch, J.-F. Méhaut, A. Neelov, S. Goedecker, J. Chem. Phys. 131, 034103 (2009).
Authors
L. Genovese and P. Bruno.
ESRF Theory Group



