Piezoelectric properties in non-polar block copolymers

While most polymers are typical dielectrics, which may exhibit paraelectric properties such as electrostriction [1], the block copolymers under study here displayed an unexpected response to applied electric fields [2]. This work presents the first study of converse piezoelectric properties in non-crystalline polymer systems, consisting of non-polar monomers, and evaluates the systems evolution with temperature to yield detailed information on an electric field–polymer interaction at a molecular level. The observed properties should hold generally and suggest that block copolymers may provide a valuable new route to piezoelectric materials.

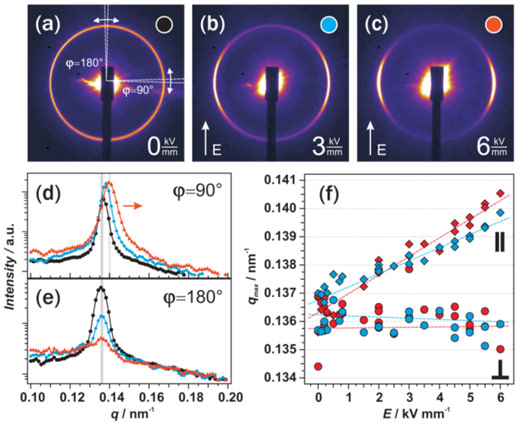
Figure 1a–c depicts representative X-ray scattering patterns of a lyotropic block copolymer solution, exhibiting a lamellar morphology, in the presence of an external electric field. Modest field intensities readily align lamellae predominantly parallel to the applied field [3,4] (Figure 1b). Higher intensities change the periodicity of parallel-oriented lamellae: their distance decreases normal to an increasing electric field [2]. This is evident from Figure 1c, which depicts the anisotropic scattering of the lamellar lyotropic phase. The analysis of scattered intensities parallel and normal to the electric field direction (Figure 1d,e) reveals that lamellae oriented parallel to the applied field are primarily affected in the phase separated state, while the periodicity of lamellae oriented perpendicular to field direction is barely altered. Both linearity and direction of the electroactive response indicate a converse piezoelectric behaviour in contrast to bare electrostriction and/or Maxwell stress due to electrostatic forces typical for paraelectric materials.

Figure 1. Raw 2-D-SAXS patterns for a 32.5 wt.% solution of poly(styrene-b-isoprene) block copolymer in toluene at 48°C (T < TODT) in the absence (a) and in the presence of an applied field of 3 kV/mm (b) and 6 kV/mm (c). Arrows indicate the direction of the electric field vector. 5° angular sections in (a) represent sectors at azimuthal angles φ=90° and φ=180°. Azimuthally averaged scattering intensity for sectors parallel (φ=90°) (d) and normal (φ=180°) (e) in the absence (black solid lines), and presence of an applied field of 3 kV/mm (blue solid lines) and 6 kV/mm (orange solid lines). Evolution of qmax with increasing electrical field intensity for lamellae oriented normal (circles) and parallel (diamonds) to the applied field (f). Data obtained from heating and cooling cycles (see principal publication) are colour coded in red and blue, respectively. Error bars are smaller than symbol size and are omitted.

To quantify the temperature-dependent electroactive response of block copolymers, the piezoelectric susceptibility κ(T), is determined from the initial slope of a linear fit to q_max(E,T) data according to Equation 1 (Figure 1f).

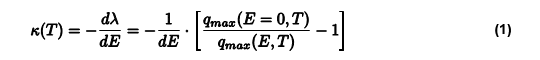
Furthermore, the piezoelectric asymmetry Γ(T), quantifying differences in electroactive behaviour independent of the initial structural orientation towards the field vector, is defined as

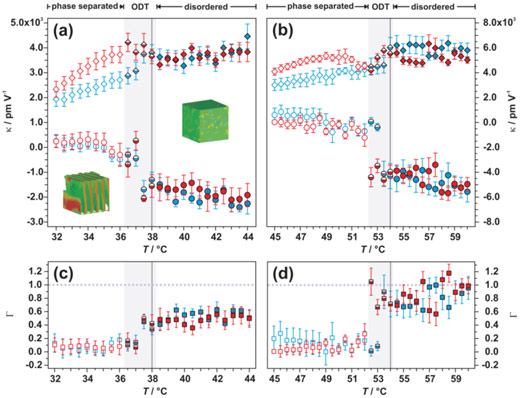
Considering the evolution of the piezoelectric susceptibility with temperature (Figure 2), three regions may be distinguished: i) For temperatures below the order-disorder transition temperature T_ODT, barely any piezoelectric effect may be discerned for perpendicular oriented lamellae, i.e., k_⊥(T < T_ODT) ≈ 0 pmV⁻¹and hence Γ(T) ≈ 0. Whereas parallel-oriented lamellae exhibit a positive piezoelectric susceptibility k_||(T<T_ODT) with magnitudes ranging from 2000–5000 pmV⁻¹; that is, the lamellar spacing decreases in the presence of an external electric field. ii) In close proximity to the order-disorder transition, k_||(T) increases significantly with temperature. Remarkably, k_⊥ becomes negative, indicating an increasing periodicity of lamellae oriented normal to the applied field. Moreover, |k_⊥(T)| converges to about the same magnitude as observed for parallel oriented lamellae and Γ(T) increases accordingly. iii) In the disordered phase, piezoelectric susceptibilities for both orientations are considerably higher in comparison to the ordered phase and converge to comparable magnitudes for higher polymer concentrations. Consequently, Γ(T) → 1 above the order-disorder transition (ODT), which indicates block copolymer chains that are increasingly more sensitive to an applied field irrespective of field orientation.

Figure 2. Evolution of the piezoelectric susceptibility with temperature for block copolymer lamellae oriented perpendicular (k⊥(T),circles) and parallel to an applied field (k||(T), diamonds) for a 30.5 wt.% (a) and 32.5 wt.% (b) solution of poly(styrene-b-isoprene) block copolymer in toluene. The insets in (b) represent simulation data of the lamellar and disordered phase (see principal publication for details). Piezoelectric asymmetry Γ(T) for both concentrations according to Eq. 2 (30.5 wt.% (c), 32.5 wt.% (d). Heating and cooling cycles are colour coded in red and blue, respectively. Empty symbols represent the lamellar phase, half-filled symbols illustrate the ODT region (also indicated by grey background shading), and filled symbols highlight data obtained in the disordered phase. The dark grey line indicates TODT for respective block copolymer solutions in the absence of an electric field and the dashed line indicates the ideal case of a symmetric electroactive response irrespective of electric field orientation.

In contrast to classical piezoelectric materials, which lose their electroactive response when the molecular structure becomes isotropic above a certain temperature, for the block copolymer system discussed herein, the piezoelectric susceptibility remains high in the vicinity of T_ODT. In fact, the highest converse piezoelectric susceptibilities are observed above ODT, where system anisotropy diminishes.

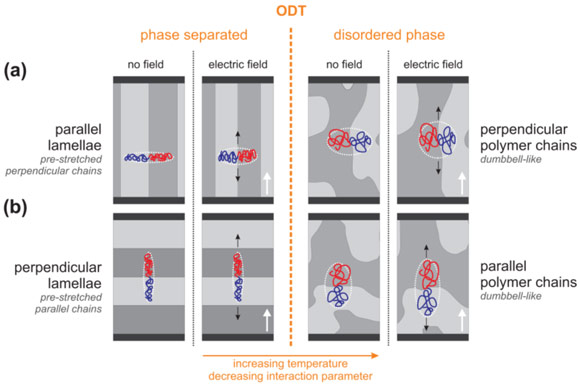
On a molecular level, for temperatures in the vicinity of ODT, nanostructures begin to disintegrate to form a disordered phase consisting of dumbbell-like polymer chains [5,6], and the enthalpic penalty for unlike monomer–monomer contacts diminishes. The more Gaussian-like chain conformation of unlike blocks is anticipated to facilitate chain distortion by an applied field without bias with respect to chain orientation (Figure 3). Indeed, the magnitudes of the piezoelectric susceptibilities involve comparable values and Γ(T) sharply increases with temperature.

Figure 3. Schematic representations of the effect of an external electric field on the polymer chain conformation below and above ODT for orientations parallel (a) and normal (b) to field direction. Black horizontal bars indicate the electrodes. Black arrows indicate the chain distortion by Kuhn segment reorientation in the presence of an applied field. The bold white arrows indicate the direction of the electric field vector.

Principal publication and authors
C.W. Pester (a), M. Ruppel (b), H.G. Schoberth (a), K. Schmidt (c), C. Liedel (a), P. van Rijn (a), K.A. Schindler (a), S. Hiltl (a), T. Czubak (a), J. Mays (d), V.S. Urban (e), A. Böker (a), Piezoelectric Properties of Non-Polar Block Copolymers, Advanced Materials 23, 4047-4052 (2011).
(a) Lehrstuhl für Makromolekulare Materialien und Oberflächen, RWTH Aachen University (Germany)
(b) Chemical Sciences Division, Oak Ridge National Laboratory (USA)
(c) Materials Research Laboratory, University of California, Santa Barbara (USA)
(d) Center for Nanophase Materials Sciences, Oak Ridge National Laboratory (USA)
(e) Neutron Scattering Science Division Oak Ridge National Laboratory (USA)

References
[1] T. Furukawa, N. Seo, Jpn. J. Appl. Phys. 29, 675 (1990).
[2] K. Schmidt, H.G. Schoberth, M. Ruppel, H. Zettl, H. Hänsel, T.M. Weiss, V. Urban, G. Krausch, A. Böker, Nature Mater. 7, 142 (2008).
[3] T.L. Morkved, M. Lu, A.M. Urbas, E.E. Ehrichs, H.M. Jaeger, P. Mansky, T.P. Russell, Science 273, 931 (1996).
[4] V. Olszowka, M. Hund, V. Kuntermann, S. Scherdel, L. Tsarkova, A. Böker, ACS Nano 3, 1091 (2009).
[5] K. Almdal, J.H. Rosedale, F.S. Bates, G.D. Wignall, G.H. Fredrickson, Phys. Rev. Lett. 65, 1112 (1990).
[6] E. Helfand, Z.R. Wasserman, Macromolecules 9, 879 (1976).

Top image: Anisotropic deformation of block-copolymer lamellae in an electric field.