Magnetite, Fe3O4, is the first magnetic material discovered and utilised by mankind in Ancient Greece, yet it still attracts attention due to its puzzling properties. Discovered in the first half of the twentieth century, the Verwey transition in magnetite [1] remains one of the most intriguing phenomena in solid-state physics. Magnetite is a ferrimagnet with an anomalously high Curie temperature TC = 850  K. Hence, it is viewed as an ideal candidate for room-temperature spintronic applications. It crystalises in the inverse spinel cubic structure, with two types of Fe sites: the tetrahedral A sites and the octahedral B ones. At TV = 124  K, a first-order phase transition occurs as the electric conductivity drops by two orders of magnitude with the simultaneous change of the crystal structure from the cubic to monoclinic symmetry and with spectacular anomalies in practically all physical characteristics. The low-temperature structure of magnetite, as deduced from recent studies, was identified to be of monoclinic Cc space group symmetry, with a complex displacement pattern [2]. This suggests that electron localisation, responsible for the dramatically increased resistivity, appears in basic three-Fe-site units, called “trimerons”.

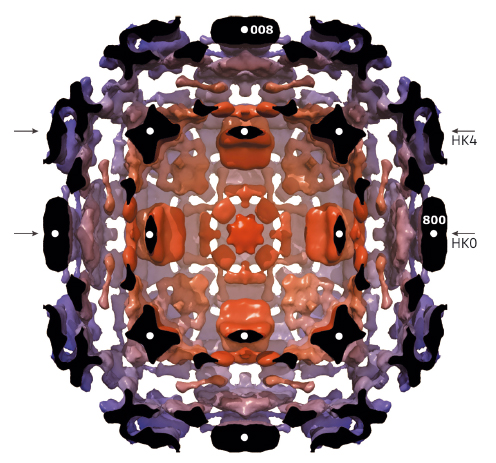Isosurface representation of diffuse scattering in magnetite

Fig. 146: Isosurface representation of diffuse scattering in magnetite slightly above TV. Colour represents the distance to the (000) node; diffuse clouds in the proximity of weak Bragg spots have been removed. The half-space above the H0L plane has also been removed. White circles mark strong Bragg reflections in the H0L plane, and arrows denote HK0 and HK4 cuts perpendicular to the image plane.

With the use of a state-of-the-art large area detector (PILATUS 6M) at beamline ID29, a detailed three-dimensional (3D) reciprocal space mapping can be performed, revealing an extremely rich diffuse scattering pattern (Figure 146), inherited from the complex low-temperature structure below the Verwey transition. Even at room temperature, which is considerably higher than the 124 K transition temperature, electrons appear to be correlated over relatively large length scales (Figure 147). The characteristic length estimated from the width of diffuse features varies from ~2 unit cells (u.c.) of the prototype cubic structure at TV+2.5  K to a value slightly larger than ~1  u.c. at room temperature. Thus, the ordering pattern cannot be reduced to the trimeron features, but rather to complexes of trimerons. Therefore, our study supports the polaron picture, and we can state that its structure is in reality much more complex than ever expected previously. We were able to associate some characteristic experimental features with the topology of the Fermi surface of magnetite. While the structure of the low-temperature phase was frequently considered as a key to the understanding of the Verwey transition, our work indicates that the diffuse scattering pattern above the transition actually encodes some key information.

Diffuse scattering in magnetite at variable temperature

Fig. 147: Diffuse scattering in magnetite at variable temperature. Magnetite reciprocal space cuts HK0 (a) and HK4 (b) are shown at room temperature (RT), slightly above (TV + δ) and below (TV − δ) the Verwey transition, with δ ~ 2.5  K. Left-hand bottom panels: Sections perpendicular to the cell doubling direction. Right-hand bottom panels: sections parallel to the cell doubling direction. Selected regions of interest (see text) are shown in (c) together with the unit cell vectors a* and b*. Cubic m3m (above TV) and tetragonal 4/mmm (below TV) Laue symmetries have been applied.

 

Principal publication and authors
A. Bosak (a), D. Chernyshov (b),  M. Hoesch (c), P. Piekarz (d),  M. Le Tacon (e), M. Krisch (a),  A. Koz?owski (f), A.M. Oleś (e,g) and  K. Parlinski (g), Phys. Rev. X 4, 011040 (2014).
(a) ESRF
(b) SNBL, ESRF
(c) Diamond Light Source, Didcot (UK)
(d) Institute of Nuclear Physics, Polish Academy of Sciences, Kraków (Poland)
(e) Max-Planck-Institut für Festkörperforschung, Stuttgart (Germany)
(f) AGH-University of Science and Technology, Kraków (Poland)
(g) Marian Smoluchowski Institute of Physics, Jagellonian University, Kraków (Poland)

References
[1] E.J.W. Verwey, Nature 144, 327 (1939). [2] A. Faber, in Spectroscopy Techniques, B. Richards, H. Evans (Eds.), Oxford University Press, New York, 1-34 (1999).