EXAFS.html

Principes de la spectroscopie EXAFS

(Extended X-Ray absorption fine structure)

 

 

A - INTRODUCTION

 

La spectroscopie d'absorption X (XAS) par les atomes est, de nos jours, un des outils les plus puissants pour l'étude des propriètés physicochimiques de la matière inerte ou vivante.

Soulignons le fait que c'est précisément la possibilité d'obtenir des sources multi longeur d'ondes et intenses de photons qui explique le développement important de cette technique lors des quinze dernières années. Ce cours sera construit comme une réelle approche de base de ce processus physique qui devrait permettre aux participants d'aborder avec confiance cette technique. Nous essaierons d'aller graduellement du plus simple vers le plus compliqué en prenant soin de bien comprendre les hypothèses simplificatrices que nous serons obligés de poser et leur domaine de vadilité.

Nous débuterons ce cours par un rappel sur la régle d'or de Fermi et l'approximation dipolaire électrique. La présentation sera simplifiée. Cependant, elle permettra de comprendre l'origine des différentes approximations qui conduisent à la formulation EXAFS standard utilisée lors de l'analyse des spectres. La suite consistera à mettre en application cette partie théorique. Nous verrons: la mise en oeuvre de la spectrométrie XAS et son analyse, comment la structure électronique d'un matériau peut être déterminée à partir des mesures de seuils d'absorption? la relation entre les oscillations présentent dans le spectre d'absorption et la structure atomique locale autour d'un élément considéré. Cette dernière partie sera étoffée par la présentation d'exemples concrets.

Le mécanisme prépondérant d'absorption des RX est l'ionisation ou effet photoélectrique. Si on néglige la diffusion cohérente et la diffusion inélastique par effet Compton, l'absorption des RX suit la même loi que la lumière traversant un milieu imparfaitement transparent (figure 1).

 

Le signal EXAFS se déduit de la mesure du coefficient d'absorption des rayons X. Ce coefficient noté (m), est une fonction de l'énergie des rayons X incidents et se calcule à partir des intensités mesurées des faisceaux incidents et transmis suivant la loi de Beer-Lambert :

I₁ = I₀ exp (- m x)

où x est l'épaisseur de l'échantillon, I₀ l'intensité du faisceau incident et I₁ l'intensité du faisceau transmis après traversée de l'échantillon. Ce coefficient (m) présente des discontinuités appelées seuils d'absorption (figure 2). Ces seuils (d'énergie notée E₀) sont liés à des transitions électroniques et sont donc caractéristiques d'un élément donné. Les seuils K, L_I, L_II,III... correspondent aux transitions d'un niveau de coeur 1s, 2s, 2p... vers un état vide situé juste au-dessus du niveau de Fermi. A basse énergie (E < E₀), la transition d'un électron du niveau de coeur n'est pas possible, le coefficient d'absorption décroît de façon monotone. Au delà du seuil (E > E₀), l'énergie d'un photon incident est suffisamment grande pour éjecter un électron (appelé photo électron) vers le continuum avec une certaine énergie cinétique (E_c). Si l'atome est isolé (gaz monoatomique), le coefficient d'absorption au delà du seuil (appelé coefficient d'absorption atomique et noté m₀) reste monotone.

 

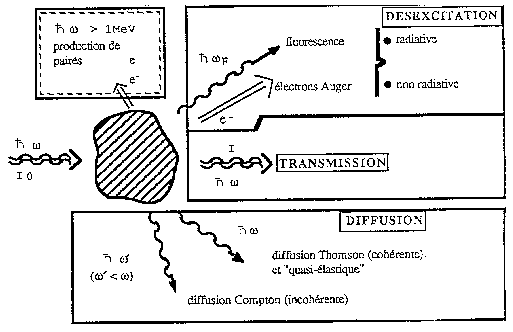
Figure 1 : Mécanisme d'absorption des RX

 

En revanche, dans le cas d'un solide, l'onde électronique sortante de l'atome central peut interférer avec celles réfléchies par les atomes voisins. Ces interférences se traduisent sur le coefficient d'absorption par la présence d'oscillations qui s'étendent sur environ 1000 eV après le seuil. Ce sont ces oscillations qui sont à l'origine du signal EXAFS. Le signal EXAFS est noté c et s'écrit :

 

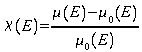
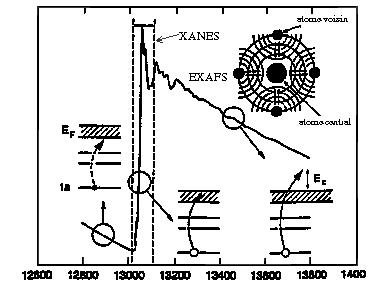
Figure 2. : Coefficient d'absorption en fonction de l'énergie des rayons X incidents

 

B - FORMULATION MATHEMATIQUE

La présentation qui suit est simplifiée. Cependant, elle permet de comprendre l'origine des différentes approximations qui conduisent à la formulation EXAFS standard utilisée lors de l'analyse des spectres.

_* La formulation du signal EXAFS suppose en premier lieu une approche semi-classique, i.e. le caractère quantique de la matière est pris en compte alors que le rayonnement électromagnétique est décrit par l'électromagnétisme classique. De plus, on suppose que seulement un électron intervient dans le processus (approximation monoélectronique) et que cet électron a une énergie cinétique suffisamment grande pour être considéré comme libre. Son énergie cinétique E_c est alors telle que

Où m_e est la masse de l'électron et k le vecteur d'onde associé à l'onde électronique. Si k est exprimé en Å^-1 et E_c en eV, la relation précédente s'écrit :

E_c = 4 k²

 

_* ^{Le coefficient d'absorption est donné par la règle d'or de Fermi :}

_|i> et _|f> sont les fonctions d'onde de l'atome dans l'état initial et final. H est l'hamiltonien d'interaction rayonnement -matière. La somme doit être effectuée sur tous les états finaux qui conservent l'énergie totale du système. Dans les expressions des fonctions d'onde et de l'hamiltonien qui seront écrites par la suite, les facteurs angulaires n'ont pas été pris en compte. Aussi l'expression du signal EXAFS obtenue à la fin de ce paragraphe ne sera valable que pour un composé isotrope.

On se place dans l'approximation dipolaire électrique : l'hamiltonien d'interaction est alors égale à r.e où e est le vecteur polarisation du champ électrique. Cette approximation reste valide tant que k_photon a<< 1 où a est la dimension de la région d'interaction. L'ordre de grandeur de la dimension de la région d'interaction est donné par l'extension spatiale des orbitales 1s qui est égale, dans le cas d'un modèle hydrogénoïde, à a₀ / Z, où a₀ est le rayon de Bohr et Z le numéro atomique. Par exemple, au seuil K du zinc (» 10 keV), k_photon - E/_öc » 5 Å^-1, a » 0.02 Å et donc k_photon a << 1.

On suppose une diffusion simple, c'est-à-dire que seuls sont pris en compte les trajets aller et retour de l'électron de l'atome central vers chacun de ses voisins. La fonction d'onde dans l'état final _|f> s'écrit comme la somme d'une fonction _|f0> décrivant l'atome central isolé et d'une perturbation _|df> due à la rétro diffusion par l'atome voisin. L'élément de matrice au premier ordre s'écrit :

où le premier terme correspond à l'absorption atomique m_0. Le signal EXAFS étant la composante oscillante, il s'exprime sous la forme :

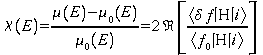
Il reste à exprimer |df> en fonction de |f₀ >.

- Lorsque le photo électron est éjecté de l'atome central, sa fonction d'onde est |f₀>. Lorsqu'il se propage vers l'atome voisin, sa fonction d'onde est de la forme H_L+(kr) où H_L+ est la fonction de Hankel sphérique. De plus, en traversant le potentiel de l'atome central, l'électron subit un déphasage d_L dû à l'interaction coulombienne. La fonction d'onde résultante de l'électron éjecté de l'atome central est donc :

|df> = |f₀> H_L+(kr) exp(i d_L)

Dans le cas d'un seuil K, la fonction d'onde initiale de l'électron est de type s (L = 0). Les règles de sélection imposant des transitions sur les états DL = ±1, la fonction d'onde dans l'état final sera de type p (L = 1). Par ailleurs, comme l'énergie du photo électron est assez grande, la fonction de Hankel est remplacée par sa forme asymptotique (kr >> 1, H_{1+ »} i exp(ikr)/2kr). A l'arrivée sur le diffuseur (soit en r = R), la fonction d'onde, notée |f₁ >, s'écrit alors :

|f₁> = |f₀>

_{- L'électron est ensuite diffusé par l'atome voisin. La fonction d'onde après diffusion contient la fonction d'onde incidente, ainsi qu'une fonction d'onde spécifique sortant de l'atome diffuseur multipliée par une fonction de diffusion f(q, k).}

La fonction d'onde après diffusion, notée |f₂>, s'écrit :

|f₂> = |f₁>

_{La fonction de diffusion est calculée en supposant que l'onde incidente est plane au lieu d'être sphérique (approximation des ondes planes). Elle s'écrit :}

où P_L' est le polynôme de Legendre d'ordre L' et d_L' le déphasage partiel créé par le potentiel de l'atome diffuseur. Dans le cas de la rétro diffusion, q=p, d'où P_L' = (-1)^L'

f(p, k) peut se mettre sous la forme : |f(p, k)| exp (i F(p, k))

où F est la fonction de phase et |f(p, k)| la fonction d'amplitude de rétro diffusion.

 

L'approximation en onde plane est aussi appelée approximation du "petit atome" ou des "hautes énergies". Une illustration en est faite sur la figure 3. L'atome diffuseur est schématisé par une sphère de rayon |f(p, k)|. La différence de phase entre le front de l'onde plane et le front de l'onde sphérique est donnée par Df = k |f(p, k)|²/R (Lee, 1975). Celle-ci est donc d'autant plus faible que |f(p, k)| est petit. De plus comme |f(p, k)| varie en 1/k, l'approximation par une onde plane est essentiellement valable quand kR est grand, c'est-à-dire quand k est grand (énergie cinétique importante) et/ou R est grand.

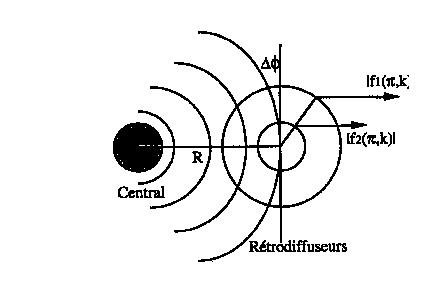
Figure 3 : Illustration de la validité du traitement en onde plane pour 2 rayons d'atomes rétro diffuseurs

 

- Lorsque l'électron revient vers l'atome absorbeur, c'est-à-dire en r = 0, il subit à nouveau le déphasage dû à l'atome central. Ce déphasage est supposé être le même qu'à l'aller, c'est-à-dire que le potentiel de l'atome central n'a pas relaxé entre le moment où le photo électron a été émis puis est revenu. Cette hypothèse reste valable tant que l'énergie cinétique est supérieure à environ 100 ev. La fonction résultante, notée |df>, est donc :

 

|df > = |f₂ (q = p, r = 0)> exp (id₁)

soit |df > = |f₀>

_{D'où comme}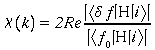

- Jusqu'à présent, nous avons considéré que l'électron ne subissait que des phénomènes élastiques et que les distances inter atomiques étaient fixes. La réalité étant différente, des termes correctifs sont introduits dans l'expression de c(k).

 

Processus inélastiques

 

Sous l'effet de la perturbation due à la création du trou, il y a une réorganisation des électrons de valence. Ces processus multiélectroniques contribuent au saut d'absorption sans intervenir dans l'EXAFS. Du fait de la normalisation des oscillations par rapport au saut, l'intensité du signal EXAFS est diminuée d'un facteur noté S₀². Ce terme décroît de 1 à 0.7 pour k < 7 Å^-1 puis est à peu près constant pour k > 7Å ¹. Il varie suivant les matériaux, mais est égal en moyenne à 0.75 (Teo, 1985).

Le photo électron ne diffuse élastiquement dans la matière que sur une distance moyenne (fonction de son énergie cinétique) correspondant au libre parcours moyen l. Pour tenir compte de cet effet, on multiplie l'expression EXAFS par un terme, purement phénoménologique, d'amortissement en exp(-2R/l(k)). Le libre parcours moyen l peut être paramétré par la formule "universelle" :

z=3,9Å^-1 et G=0,53Å^-2 pour les matériaux inorganiques (Teo, 1981)

Dans le domaine de l'EXAFS (k > 3Å^-1 soit E_c > 36 eV), le libre parcours moyen varie linéairement avec k et est très faible (quelques Å) (figure 4). Cette propriété fait donc de l'EXAFS une sonde très locale.

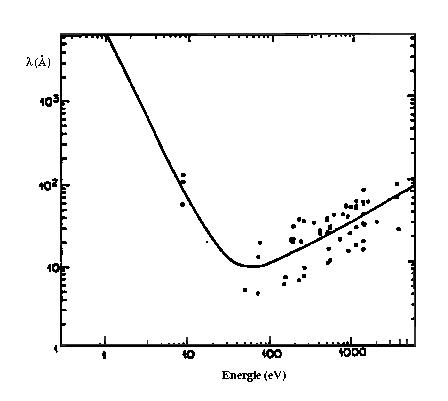
Figure 4 : Libre parcours moyen de l'électron en fonction de son énergie cinétique

 

Distribution de distances

 

Les distances inter atomiques R sont soumises à des fluctuations dues à l'agitation thermique et au désordre structural. La formulation EXAFS classique suppose que la distribution de distances, engendrée par le désordre d'origine thermique et structurale, est une gaussienne de largeur s. Le désordre intervient alors dans le signal EXAFS comme un terme en exp (- 2s²k²). s est appelé facteur de Debye-Waller, par analogie à la diffraction X, représente ici la distribution de distances atome central - atome voisin. Si les mouvements de l'atome central et de l'atome voisin sont corrélés et en phase, le facteur de Debye-Waller sera faible même si le déplacement absolu de chacun des atomes est important.

 

_* ^{L'expression du signal EXAFS s'écrit finalement :}

Cette expression est valable pour une paire atomique (atome central + atome rétro diffuseur). On montre qu'au sein d'un échantillon les contributions de chacun des atomes voisins sont additives. Si on définit une couche atomique comme l'ensemble des atomes (N_i) qui sont de nature chimique identique (i) et à la même distance de l'atome central (R_i) alors le signal EXAFS total s'écrit comme la somme sur toutes les couches (i) de signaux EXAFS partiels, soit :

 

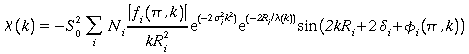
En résumé, les différentes hypothèses conduisant à cette formule sont :

- un électron éjecté d'un seuil K (un état initial L = 0 et un seul état final L = 1)

- la rétro diffusion ou diffusion simple (fonction de diffusion f (q,k) prise à q = p

- un traitement en onde plane (f(q,k) indépendant de R)

- un composé isotrope

- une distribution harmonique des distances (facteur de désordre en exp(-2 s²k²))

 

 

C - MISE EN OEUVRE EXPERIMENTALE

Le coefficient d'absorption se mesure classiquement en enregistrant l'intensité du faisceau avant et après traversée de l'échantillon. Ces expériences nécessitant un flux de photons important, elles sont le plus souvent réalisées avec le rayonnement synchrotron. Quel que soit l'anneau sur lequel on travaille, un montage expérimental de base est constitué d'un monochromateur et de deux détecteurs placés avant et après l'échantillon (figures 5.a et 5.b).

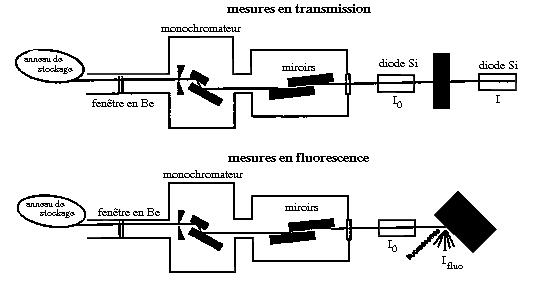
Figure 5.a : Montages expérimentaux en transmission et en détection de fluorescence

 

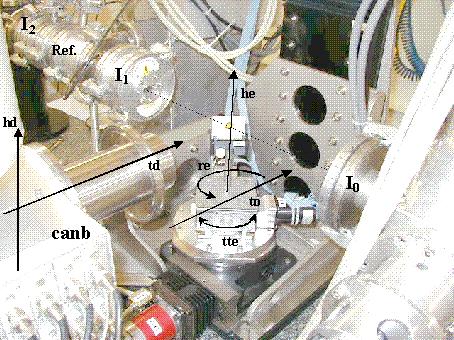
Figure 5.b : Montage expérimental sur la ligne BM32

D - ANALYSE DE DONNEES

Lors d'une expérience, le signal obtenu est le coefficient d'absorption du matériau µx (où x est l'épaisseur de l'échantillon en fonction de l'énergie. La première étape de l'analyse consiste à déterminer le signal EXAFS c(k). Ce signal est une somme de plusieurs termes et nous cherchons à déterminer les paramètres N_i et R_i. La plupart des programmes d'analyse de données permettent d'accéder à ces paramètres par une technique de filtrage de Fourier (transformée de Fourier directe puis inverse). Le signal résultant de cette procédure est un spectre EXAFS partiel qui correspond à la contribution d'une ou plusieurs couches atomiques au spectre EXAFS total. Le nombre de paramètres à déterminer est alors réduit, ce qui facilite l'analyse. Ils sont obtenus par ajustement par moindres carrés.

D.1 - OBTENTION DE c (k)

Lors d'une expérience, les données enregistrées sont les intensités avant (I₀) et après échantillon (I) en fonction de l'énergie E. Le coefficient d'absorption est calculé par si l'expérience s'est déroulée en transmission et par si il s'agit d'une détection de fluorescence (FY) ou d'électrons (TEY ou CEY). Le signal EXAFS s'exprime théoriquement à partir de µ comme ou comme où µ₀ est l'absorption atomique. Or le coefficient d'absorption expérimental contient l'absorption de la matrice (µ₁). Cette absorption étant quasiment constante sur tout le domaine en énergie, elle équivaut à un fond continu qui doit être soustrait au coefficient d'absorption µ. Le signal EXAFS s'écrira donc :

Théoriquement, la formule EXAFS s'exprime comme une fonction de k. Sur le signal expérimental, il est donc nécessaire de transformer les énergies en vecteurs d'onde. Cette transformation s'opère par la relation , ce qui nécessite la détermination de E₀. L'énergie du seuil est choisie arbitrairement, soit au maximum de la dérivée, soit à la mi-hauteur du saut d'absorption. Généralement, elle est prise à mi-hauteur pour plus de reproductibilité puisque le point d'inflexion est variable selon les structures existant dans le seuil. Ce choix reste néanmoins arbitraire. En conséquence, la valeur de E₀ sera affinée lors des ajustements.

L'absorption atomique (µ₀) est généralement modélisée par une fonction spline cubique ou un polynôme ou même un filtre Fourier (figure 6a).

 

D.2 - FILTRAGE DU SIGNAL PAR DOUBLE TRANSFORMEE DE FOURIER

La première transformée de Fourier du signal EXAFS est effectuée de l'espace des k vers l'espace des distances. c(k) étant une fonction fortement décroissante en k à cause des fonctions du libre parcours moyen et du facteur de Debye-Waller. Le signal est multiplié préalablement par une puissance de k (1, 2 ou 3). La puissance sera choisie de façon à renforcer le signal à haut k sans pour autant accroître l'amplitude du bruit.

Le calcul d'une transformée de Fourier conduit à l'obtention de deux fonctions qui sont la partie réelle et la partie imaginaire. Généralement, on représente le module qui est aussi appelé fonction de distribution radiale (FDR) (figure 6c). La FDR présente plusieurs pics centrés à des distances R'_i et dont l'amplitude est proportionnelle au nombre de voisins N_i.

Par ailleurs, les distances R'_i sont décalées par rapport aux distances cristallographiques R_i, du fait des déphasages f_i et d_i intervenant dans le sinus.

La suite du traitement consiste à sélectionner un ou plusieurs pics de la transformée de Fourier et à en effectuer la transformée de Fourier inverse (figure 6 d). Le signal obtenu dans l'espace des k est un signal EXAFS partiel associé à la (ou les) couche(s) atomique(s) sélectionnée(s) dans l'espace direct. Ce signal c_p(k) est caractérisé par la fréquence des oscillations ainsi que par sa courbe enveloppe (A(k)) de la formule EXAFS. Il est possible de simuler ce spectre filtré par une fonction théorique. L'affinement est effectué grâce à un programme de minimisation du carré des écarts.

 

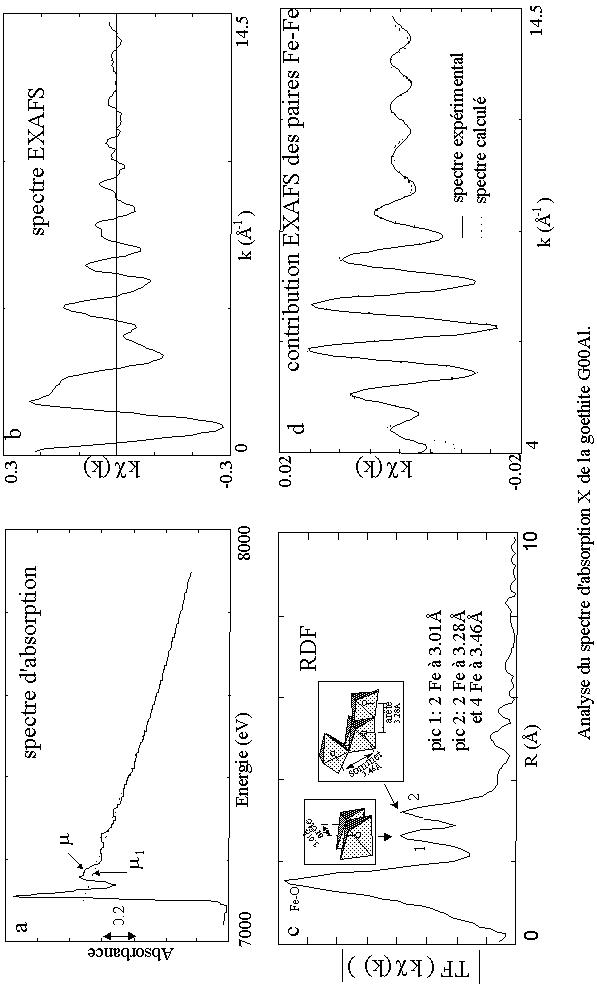
Figure 6 : Etapes de l'analyse de données

 

D.3 - PARAMETRES

L'expression du signal EXAFS partiel c_p(k) ne porte que sur quelques couches atomiques (i). Elle s'écrit donc :

^{(1) :}

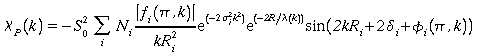
et peut se mettre sous la forme équivalente :

(2) :

La formule (1) permet de distinguer deux groupes de paramètres ; d'une part des termes structuraux (R, N, s, l) et d'autre part, des termes électroniques (|f(p, k)|, F, d₁). Ces derniers paramètres ont été soit calculés ab initio, auquel cas ils sont tabulés, soit établis à partir de références cristallines. Ils seront discutés au paragraphe D.3-b. Par identification à la formule (1), la formule (2) conduit à classer les différents paramètres en termes d'amplitude (R, N, ,s, l, |f(p, k)|) et en termes de phase (R, F, d₁). Les termes structuraux sont tous des paramètres ajustables et déterminés à l'issue de l'affinement. Leur influence sur l'amplitude et la phase de la courbe calculée est discutée ci-dessous.

D.3.a - Termes structuraux

Paramètres d'amplitude : R, N, s, l

s et l jouent sur l'enveloppe de c(k) (A(k)). Le terme contenant s est en exp(-2s²k²). Quand s augmente, l'amplitude de la courbe calculée s'amortit rapidement à haut k. Le terme contenant l est en exp( 2r/l) ou l peut être considéré comme une fonction linéaire en k pour k ³ 3 Å^-1. Son expression est alors l = 2k/g ou g est une constante. Lorsque g augmente, l'amplitude de la courbe calculée diminue, mais cette fois surtout à bas k. N et R jouent simplement comme des facteurs d'échelle. Bien que leur dépendance en k soit différente, tous ces paramètres sont néanmoins fortement corrélés.

Paramètres de phase : R, DE₀

Le terme de phase est en . En première approximation, les fonctions de phase f_i et d_i dépendent linéairement de k, elles peuvent donc s'écrire sous la forme (2 ak + b). La période des oscillations est donc égale à si bien qu'à une augmentation de distance correspond un accroissement de la fréquence. Lors de l'ajustement de la phase, on ajoute un paramètre DE₀. Celui-ci permet de translater en énergie la courbe calculée afin de compenser une mauvaise évaluation de E₀. L'énergie du seuil est reliée à k par . La variation d'énergie DE₀ est donc proportionnelle à -k.Dk. Une augmentation de ce terme se traduira par un décalage vers les faibles valeurs de k d'autant plus important que k est petit.

Toutes ces considérations ne sont valables que dans le cas d'une contribution unique. En effet, dès lors qu'il existe plusieurs paires atomiques, les termes de phase entraînent des interférences sur le signal EXAFS et les effets précédemment décrits pour chacun des paramètres sont plus complexes. La présence de contributions multiples est aisément visualisée sur le spectre EXAFS partiel. Lorsque deux contributions existent, le signal présente un accident dans sa phase appelé "battement". Les battements sont situés à des valeurs de k telles que k = np/2DR (n entier ¹ 0) où DR est l'écart entre les distances de chacune des paires atomiques. En pratique, la valeur maximum de k étant égale à 14 Å^-1, deux contributions seront discernables si DR est au minimum de 0.11-0.13 A. Si l'écart entre deux distances est inférieur à cette valeur, il n'est pas raisonnable d'ajuster le spectre expérimental avec deux contributions. Dans le cas contraire, il faudra prendre garde au nombre de paramètres indépendants ajustables (N_ind) est limité. Il a été établi (Cortès, 1988) que ce nombre devait être tel que :

où dR' est l'intervalle entre les bornes sélectionnées pour la transformée de Fourier inverse et dk est le domaine sur lequel s'effectue l'ajustement. Si dR' = 1.5 Å, dk = 8 Å^-1, l'application numérique conduit à Nind » 8. Avec deux contributions, le nombre de paramètres est de 10 (5x2) et excède N_ind. Il est donc nécessaire de limiter le nombre de variables. Nous avons vu précédemment que les paramètres d'amplitude (N, s et l) étaient fortement corrélés, ils ne sont donc pas ajustables simultanément. Contrairement au nombre de voisins et au facteur de Debye-Waller, le libre parcours moyen est à peu près constant pour des composés dont l'environnement chimique et structural est proche. L est donc déterminé pour une paire atomique donnée à partir de références cristallines puisque, dans ce cas, R et N sont connu grâce à la diffraction. Cette valeur est ensuite laissée fixe lors de l'affinement des autres paramètres du composé inconnu. Par ailleurs, comme nous l'avons vu précédemment, DE₀ permet de rattraper les erreurs de détermination de l'énergie de seuil. Ce paramètre est donc ajustable mais il est supposé identique pour toutes les paires atomiques. Le nombre de paramètres ajustables pour p couches est donc égal à 3p + 1. Si cette valeur est encore supérieure à celle du nombre de paramètres indépendants, alors il est possible de laisser les facteurs de Debye-Waller identiques de sorte à réduire encore le nombre de paramètres ajustables à 2p+2.

D.3.b - Termes électroniques

Ils peuvent provenir de calculs ab initio, ou sont extraits du spectre EXAFS de références cristallines.

Références cristallines :

Dans le cas de références cristallines, on fait l'hypothèse dite de transférabilité. Ceci suppose que les potentiels sont indépendants de la liaison chimique et que leur variation en fonction du degré d'oxydation du diffuseur peut être compensée par un décalage en énergie DE₀. La fonction de diffusion est alors considérée comme indépendante de l'état chimique du composé. Cette hypothèse est équivalente à dire que l'électron est diffusé par le coeur du potentiel atomique et ne voit donc pas les électrons de valence situés à la périphérie. Ceci est justifié dans le domaine de l'EXAFS puisque l'énergie du photo électron est grande devant les énergies de liaison.

En pratique, le spectre EXAFS de la référence cristalline est filtré pour obtenir le spectre EXAFS partiel d'une contribution c_p(k). Les termes structuraux de la contribution R et N sont connus à partir de données cristallographiques. Le libre parcours moyen et le facteur de Debye-Waller sont déterminés par ajustement en utilisant des fonctions de phase et d'amplitude théoriques. L'ensemble de ces termes étant fixé, on connaît alors A(k)/|f(p, k)|. A(k) correspondant à l'amplitude du spectre expérimental, on en déduit |f(p, k)|. De façon similaire, comme le déphasage expérimental total est connu à partir du spectre EXAFS partiel et que la distance est donnée par la cristallographie, il est aisé d'extraire 2d+f(k). La fonction de phase expérimentale contient le déphasage lié à l'atome central (d) et la fonction de phase liée au rétro diffuseur (f(k)) ; elle n'est donc utilisable dans le cas de composés inconnus que pour une même paire central-rétrodiffuseur. La détermination des fonctions de phase et d'amplitude expérimentales n'est possible que dans le cas où la paire atomique filtrée lors de la transformée de Fourier est unique. Or deux contributions ne sont pas séparables sur les pics de la transformée de Fourier si elles sont trop proches. Il est délicat de fixer une valeur limite de séparation puisqu'elle va dépendre de la nature du voisin, des amplitudes relatives des contributions et des paramètres utilisés lors de la transformée de Fourier (type de fenêtre, t, n, dk). En première approximation deux contributions seront séparables si la distance entre deux pics de la transformée de Fourier est au moins égale à la largeur d'un pic, soit DR' = 2p/dk où DR' est la largeur du pic principal de la transformée de Fourier d'une fonction "porte". Si les voisins sont de nature identique, cela correspondra à un écart de distances de DR - DR' » 0.6 Å (pour dk = 10 Å-1). Dans le cas où les contributions ne sont pas séparables, on a alors recours à des amplitudes et déphasages théoriques calculés ab initio.

Fonctions théoriques

Trois auteurs ont publié des fonctions théoriques : Teo et Lee (1979), Mc Kale et al. (1988), Rehr et al. (1991). Elles résultent d'hypothèses différentes :

Teo et Lee (1979) utilisent l'approximation des ondes planes comme décrit en II-A. Les fonctions de rétro diffusion sont alors indépendantes de R. L'approximation en onde planes étant mauvaise à bas k, des erreurs sur la détermination des distances sont à craindre surtout dans le cas d'atomes légers pour lesquels les fonctions de rétro diffusion sont centrées à bas k. Il est donc préférable d'utiliser d'autres tables.

La formulation complète en ondes sphériques a été donnée par Lee et Pendry (1975) et Ashley et Doniach (1975). Mc Kale et al. (1986, 1988) utilisent cette formulation dans l'hypothèse de la rétro diffusion simple. Dans ce cas, la formulation de l'EXAFS en onde sphérique a ceci de particulier qu'elle est identique à celle de l'EXAFS en onde plane en remplaçant les fonctions diffusion par des fonctions dépendantes de la distance inter atomique. La formulation classique n'apparaît plus alors comme une approximation, mais comme la formule rigoureuse en ondes sphériques dans l'approximation de la rétro diffusion simple. Les phases (f_i et d_L) et les amplitudes ont été tabulées pour tous les éléments aux seuils K et L, pour deux distances central-rétrodiffuseur égales à 2.5 et 4 Å. Lors des ajustements, ces phases et ces amplitudes sont déterminées pour chacune des distances inter atomiques par interpolation (de la forme a/R + b où a et b sont déterminés à partir des courbes à 2.5 Å et 4 Å).

Les fonctions d'amplitudes décroissent de façon monotone avec k pour les éléments légers puis présentent un maximum qui se décale vers les grands k quand Z augmente (figure 7a). Pour les éléments lourds, il existe plusieurs maxima qui sont situés dans le cas du plomb à 5 et 12 A-1 (figure 7b). Les fonctions de phase des rétro diffuseurs décroissent de façon monotone sauf pour les éléments lourds (figures 7c et 7d). Les variations de phase et d'amplitude en fonction de la distance sont surtout importantes à bas k, alors qu'à grand k elles tendent vers les mêmes valeurs. Ceci est normal puisque dans le domaine des grands k, l'approximation en onde plane est correcte. La différence entre les fonctions calculées à 2.5 et 4 A s'accroît lorsque le numéro atomique augmente. Les déphasages des atomes centraux sont toujours des fonctions décroissantes et monotone (figure 8). Mc Kale et al. (1988) ont repris les valeurs des déphasages centraux calculés par Teo et Lee (1979).

Les fonctions de phase (rétro diffuseur ou central) et d'amplitude sont similaires pour deux atomes de numéro atomique proches. Il est donc très difficile de différencier, par exemple, un voisin carbone d'un voisin oxygène ou un voisin fer d'un voisin manganèse, alors qu'il est aisé de reconnaître un voisin manganèse d'un voisin oxygène. Cette différenciation peut s'effectuer sur la courbe enveloppe du spectre EXAFS partiel (A(k)) qui reflète la nature des atomes (A(k) a |f(p, k)|).

 

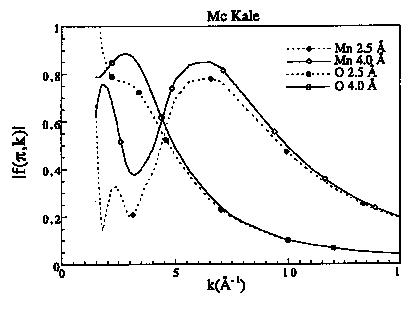
Figure 7a : Fonctions d'amplitude de rétro diffusion pour le manganèse et l'oxygène à 2.5 et 4.0 Å

 

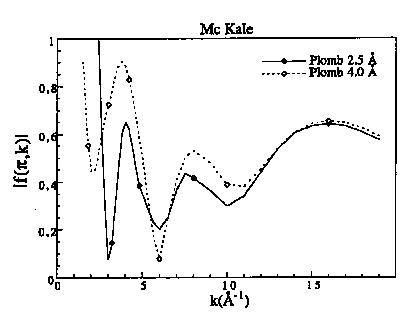
Figure 7b : Fonctions d'amplitude de rétro diffusion pour le plomb à 2.5 et 4.0 Å

 

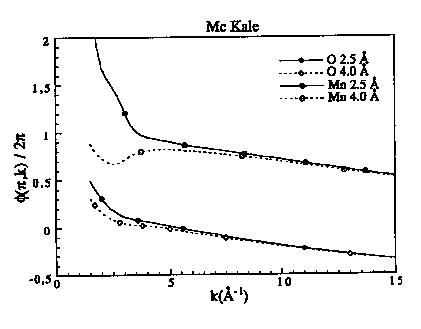
Figure 7c : Fonctions de phases de rétro diffusion pour le manganèse et l'oxygène à 2.5 et 4.0 Å

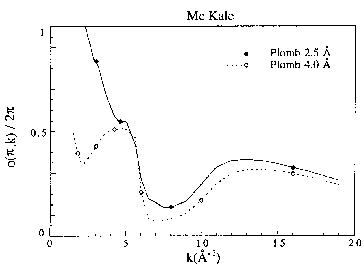
Figure 7d : Fonctions de phases de rétro diffusion pour le plomb à 2.5 et 4.0 Å

 

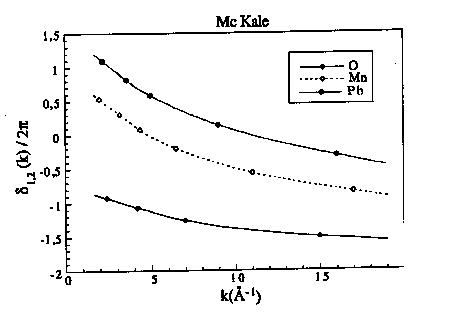
Figure 8: Déphasage central pour l'oxygène, le manganèse et le plomb tabulé par Mc Kale et al. (1988) et Teo et Lee (1979)

 

Rehr et al. (1991) et Mustre de Leon et al. (1991) utilisent les ondes sphériques et choisissent dans l'expression du potentiel un terme complexe qui prend en compte les interactions du photo électron avec les électrons environnants (effets à N corps) et qui est donc fonction de l'énergie du photo électron. Ce modèle théorique permet de déterminer les phases, les amplitudes et aussi le libre parcours moyen de l'électron. Les fonctions de phases et d'amplitudes tabulées par Rehr ont été calculées à deux distances central rétro diffuseur : 2 et 3 Å. La comparaison de la fonction d'amplitude de rétro diffusion du plomb tabulée par Mc Kale et Rehr est donnée en figure 9. Les extrema de ces fonctions se superposent aux mêmes valeurs de k, mais l'amplitude de la fonction publiée par Rehr est plus faible pour k > 4 Å^-1, alors qu'elle augmente considérablement pour k < 4 Å^-1.

 

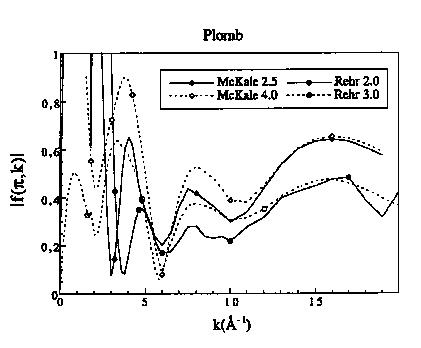
Figure 9: Fonctions d'amplitude du plomb tabulées par Mc Kale et al. (1988) et Rehr et al. (1991)

 

Plutôt que d'utiliser des fonctions de phase et d'amplitude tabulées, il est possible d'utiliser le code "FEFF" mis au point par Rehr et al. (1991) pour calculer le spectre EXAFS d'un solide quelconque (cf. également Mustre de Leon et al. 1979), L'agitation thermique est prise en compte par un modèle corrélé de Debye (Sevillano et al. 1979), ce qui suppose de connaître la température de Debye du corrélé de Debye du composé en question, ce qui n'est généralement pas le cas. Le plus souvent, le facteur de Debye-Waller demeure donc un paramètre inconnu. Ce code permet également de calculer les fonctions de phases et d'amplitudes pour une paire atomique donnée, ainsi que le libre parcours moyen. La comparaison de ces fonctions pour différentes structures permet d'évaluer leur transférabilité d'un composé à l'autre. Les figures 10 et 11 comparent les différentes fonctions d'amplitude de rétro diffusion pour des voisins oxygène et plomb dans les oxydes de plomb a et b PbO ainsi que dans la quensellite (PbMnO₂OH). Ces fonctions d'amplitude sont comparées à celles tabulées par Rehr. Pour l'oxygène, la fonction d'amplitude tabulée par Rehr est fortement différente de celles déterminées dans les structures d'oxydes. La fonction d'amplitude dans la structure a-PbO est identique à celle déterminée dans la structure b-PbO et légèrement différente de celle trouvée pour la quensellite. Pour le plomb, les différences sont moindres, sauf pour k < 4 Å^-1. Ce programme permet également de prendre en compte la diffusion multiple, ce qui est très important dans les structures où les paires atomiques sont alignées ou quasiment alignées. En effet, l'amplitude de rétro diffusion varie en fonction de l'angle q = 0°, devient environ moitié pour q »15° et chute considérablement pour q »30° (Teo et Lee, 1985).

 

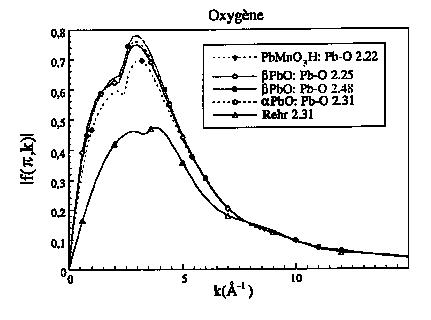
Figure 10 : Fonctions d'amplitude de l'oxygène tabulées et calculées par FEFF dans différents composés

 

Figure 11: Fonctions d'amplitude du plomb tabulées et calculées par FEFF dans différents composés

CONCLUSION

 

 

Un des avantages de la méthode EXAFS est de pouvoir sélectionner un élément par le choix de l'un de ses seuil d'absorption et d'étudier son environnement local. C'est une sonde chimique et locale.

Cette méthode est applicable à tous les matériaux, qu'ils soit cristallisés, amorphes ou liquides.

Elle constitue une méthode complémentaire à la diffraction. De plus en plus, les systèmes à étudier nécessitent le couplage à la fois de l'EXAFS et d'une méthode permettant d'avoir une autre sélectivité:

 

- le SEXAFS ou REFLEXAFS liant l'absorption X à la réflectivité pour l'étude de dépôts en surface.

- le DAFS liant l'absorption X à la diffraction pour l'étude de sites cristallographiques bien déterminés.

 

 

 

BIBLIOGRAPHIE

 

 

OUVRAGES GENERAUX TRAITANT DE L'EXAFS

 

Basic principles and data analysis, B. K. Teo (1985),

Springer Verlag, Berlin Heidelberg, New-York, Tokyo

 

Rayonnement synchrotron dans le domaine des rayons X

J. Petiau, G. Krill, P. Lagarde, Ecole d'Aussois, CNRS (1986)

 

X-Ray absorption - Principles, applications, techniques of EXAFS, SEXAFS and XANES

E. A. Stern, P. H. Durham, S. M. Heald, D. C. Koningsberger

Ed. Koningsberger and Prins, John Willey and sons (1988)

 

X-Ray Absorption Spectroscopy, A. Fontaine

Cours Hercules, Vol. 1, Ch. XV, p.323 (1994)

Ed. J. Baruchel, J.L. Hodeau, M.S. Lehmann, J.R. Regnard, C. Schlenker

 

ARTICLES

C. A. Ashley, S. Doniach, Phys. Rev. B, 11 (1975) 1279

 

R. Cortès, Ecole du CNRS "Structures fines d'absorption X : des données expérimentales à leur analyse", Garchyt (1988)

 

J. Goulon, C. Goulon-Ginet, R. Cortes, J. M. Dubois, J. Physique, 43 (1982) 539

 

P. A. Lee, G. Beni, Phys. Rev B, 15 (1977) 2862

 

P. A. Lee, J. B. Pendry, Phys. Rev. B? 11 (1975) 2795

 

A. G. Mc Kale, S. K. Chan, G. S. Knapp, Phys. Rev. B, 33 (1986) 841

 

A. G. Mc Kale, B. W. Veal, A. P. Paulikas, S. K. Chan, G. S. Knapp, J. Am. Chem. Soc., 110 (1988) 3763

 

J. J. Rehr, J. Mustre de Leon, S. I. Zabinsky, R. C. Albers, J. Am. Chem. Soc., 113 ( 1991) 5135

 

E. Sevillano, H. Meuth, J. J. Rehr, Phys. Rev. B, 20 (1979) 4908

 

B. K. Teo, P. A. Lee, J. Am. Chem. Soc., 101 (1979) 2815

 

B. K. Teo (1985), Basic principles and data analysis, Springer Verlag

Berlin, Heidelberg, New-York, Tokyo