- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Magnetism
- Determination of the Orbital Moment of CoO using Spin-resolved Photoemission
Determination of the Orbital Moment of CoO using Spin-resolved Photoemission
Transition metal materials exhibit a wide range of fascinating magnetic and electronic properties. The spin-orbit interaction often plays an important role, for example, in determining the orientation of the magnetic moments relative to the crystal axes. The measurement of the separate spin and orbital contributions to the magnetic moments is, however, far from trivial. Besides the sum rules for magnetic soft X-ray absorption dichroism (for ferromagnetic materials) and magnetic X-ray scattering (for magnetically ordered antiferromagnetic systems like NiO [1]), we have explored the feasibility of another spectroscopic technique, potentially applicable to antiferromagnets and ferromagnets. Spin-resolved photoemission using circularly-polarised soft X-rays can provide quantitative information on the magnetic moments both in ordered and disordered systems.
By measuring the spin-resolved spectra of the valence states, and by integrating over the whole valence states we can determine the total difference between photoelectrons having parallel and antiparallel alignment of their spin with the photon angular momentum. We call ![]() the ratio between this integrated difference and the integrated valence band photoemission intensity. We take advantage of the sum rule derived by van der Laan and Thole [2], which relates
the ratio between this integrated difference and the integrated valence band photoemission intensity. We take advantage of the sum rule derived by van der Laan and Thole [2], which relates ![]() to the expectation value of a spin-orbit operator of the system in the initial state. If the measurement is made on a single magnetic domain (ferromagnetic or antiferromagnetic) the sum rule can be used to estimate directly the orbital magnetic moment (under some assumptions): <Lz>
to the expectation value of a spin-orbit operator of the system in the initial state. If the measurement is made on a single magnetic domain (ferromagnetic or antiferromagnetic) the sum rule can be used to estimate directly the orbital magnetic moment (under some assumptions): <Lz> ![]() C
C![]()
![]() , where the value of C is known. If the sample can be considered as magnetically isotropic (multi-domain, or in a paramagnetic phase) then the measured quantity P can be related (having satisfied the appropriate conditions) to the ratio <Lz>/<Sz>.
, where the value of C is known. If the sample can be considered as magnetically isotropic (multi-domain, or in a paramagnetic phase) then the measured quantity P can be related (having satisfied the appropriate conditions) to the ratio <Lz>/<Sz>.
As shown in Figure 79 we have tested the technique for CoO at beamline ID12B. CoO is an antiferromagnetic insulator with an intriguing magnetic structure. The sample was a single crystal kept at T = 390 K, above TNéel. Panel a) shows the sum of the two spin polarised spectra (one with parallel and one with antiparallel orientation of the photon angular momentum and photoelectron spin). Panel b) shows their difference and panel c) gives the ratio of the integrals of the curves shown in panels a) and b). The curve in panel c) converges (going from the Fermi level EF towards higher binding energies) to the quantity ![]() = 0.045 ± 0.005. Applying the above mentioned sum rule for the isotropic cases we can thus get a rough estimate of <Lz>/<Sz>
= 0.045 ± 0.005. Applying the above mentioned sum rule for the isotropic cases we can thus get a rough estimate of <Lz>/<Sz> ![]() 0.84 at 390 K, directly from the measurements.
0.84 at 390 K, directly from the measurements.
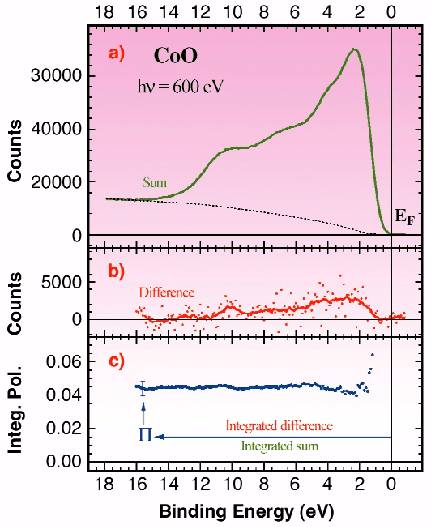 |
Fig. 79: Spin polarised photoemission spectrum of CoO measured with circularly polarised light (h
|
In order to extract further numbers, as far as local properties are concerned, we have performed model calculations using a CoO6 cluster in Oh symmetry [3]. By fine tuning the 10Dq crystal field value we were able to accurately reproduce the experimental value at T = 390 K. By combining the calculations results with the known total magnetic moment of 3.81 µB (at 0 K) we can easily derive <Lz> = 1.31![]() and <Sz> = 1.25
and <Sz> = 1.25![]() .
.
In conclusion, we have used spin-resolved photoemission to evaluate the orbital and spin moments of the antiferromagnetic compound CoO. The derivation of these quantities, in the case of transition metal magnetic insulators, can be made directly with an approximate procedure, or through the cluster model calculations simulating the photoemission experiment. The possible extension of the technique to metallic systems requires further studies.
References
[1] V. Fernandez et al., Phys. Rev. B 57, 7870 (1998).
[2] G. van der Laan and B. T. Thole, Phys. Rev. B 48, 210 (1993).
[3] A. Tanaka and T. Jo, J. Phys. Soc. Jpn. 63, 2788 (1994).
Principal Publication and Authors
G. Ghiringhelli (a,b), L. H. Tjeng (c), A. Tanaka (d), O. Tjernberg (a,e), T. Mizokawa (c,f), J. L. de Boer (c) and N. B. Brookes (a), Phys, Rev. Lett., submitted.
(a) ESRF
(b) Politecnico di Milano (Italy)
(c) University of Groningen (The Netherlands)
(d) Hiroshima University (Japan)
(e) KTH, Stockholm (Sweden)
(f) University of Tokyo (Japan)



