Although liquid crystals have been known since the end of the 19th century, they continue to surprise us with their variety of low-dimensional phases and phase transitions. In the smectic-A phase, the elongated molecules are organised in stacks of liquid layers in which the long molecular axes are, on average, parallel to the layer normal. Hence a periodic structure exists in one dimension while the system remains fluid in the other two directions. The reduced dimensionality of the translation order leads to strong thermal fluctuations of the layers, with their mean-square displacements diverging logarithmically with the sample size. Smectic liquid crystals can be suspended over an opening in a solid frame. The surface area of such a smectic membrane can be as large as several cm2, while the thickness can be varied from thousands of layers (tens of µm) down to two layers (about 5 nm). Smectic membranes constitute ideal model systems to investigate fundamental aspects of fluctuations. The finite thickness changes the continuous bulk response spectrum into discrete response modes. The dynamics of these fluctuations are accessible by coherent X-ray scattering.

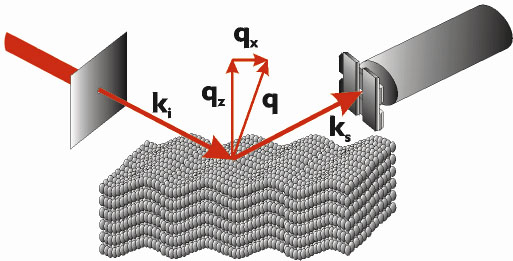Fig. 58: Schematic scattering configuration for experiments on fluctuating smectic membranes.

 

The work has been carried out at beamline ID10A. Smectic membranes were mounted in a horizontal scattering geometry (Figure 58) and illuminated by a small, 10 µm in size, partially coherent, 8 keV X-ray beam. If coherent radiation is incident on a random medium, the scattered intensity shows a speckle pattern that reflects the instantaneous arrangement of the scattering centres. Information about the dynamics of the scatterers is accessible by X-ray photon correlation spectroscopy (XPCS), in which the time dependent intensity auto-correlation function of the speckle pattern is measured. The experiments were performed in the uniform filling mode of the ESRF storage ring; by applying fast avalanche photodiode detectors, a technical lower cut-off of ~ 40-50 ns of the correlation functions was obtained. In principle, this number can be reduced to a few ns, the limit being given by the 2.8 ns electron bunch-to-bunch interval in the storage ring. Early XPCS measurements of smectic membranes employing soft X-rays indicated an exponential decay of the correlation functions with a relaxation time in the range of tens of µs [1]. The XPCS setup described here allows observation of relaxation times well below 1 µs. In addition to the exponential decay of the correlation function, an oscillatory regime of fluctuation damping was observed for thin membranes (Figure 59). Thanks to the perfect match between the millidegree mosaicity of the membranes (Figure 59, inset) and the high resolution of the setup, count rates up to 150 MHz were reached. This facilitated XPCS measurements at off-specular positions by rocking the sample, which leads to disappearance of the oscillatory damping. The correlation functions were fitted to the expression aS2(t) + b, where S(t) is the dynamic structure factor. The results are shown as the full lines in Figure 59 and are in good agreement with recent theoretical predictions [2]. These experiments open a new area for studying fast relaxations, particularly for complex membrane systems relevant to life sciences.


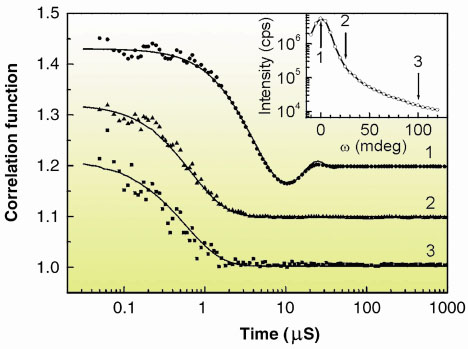Fig. 59: Autocorrelation functions of 2.83 µm thick membrane of the compound FPP at the specular position (1) and at off-specular positions (2, 3); (Inset) Rocking curve around the Bragg position with the various settings. Curves 1 and 2 are shifted for clarity (by 0.2 and 0.1, respectively).

 

References
[1] A.C. Price, L.B. Sorensen, S.D. Kevar, J. Toner, A. Ponierewski and R. Holyst, Phys. Rev. Lett., 82, 755-758 (1999).
[2] A.N. Shalaginov and D.E. Sullivan, Phys. Rev. E, 62, 699-710 (2000).

Principal Publications and Authors
A. Fera (a), I.P. Dolbnya (b), G. Grübel (c), H.G. Muller (a), B.I. Ostrovskii (a, d), A.N. Shalaginov (e) and W.H. de Jeu (a), Phys. Rev. Lett., 85, 2316 (2000); I. Sikharulidze (a), I.P. Dolbnya, A. Fera, A. Madsen (c), B.I. Ostrovskii and W.H. de Jeu, Phys. Rev. Lett. (in press).
(a) FOM-Institute for Atomic and Molecular Physics, Amsterdam (The Netherlands)
(b) DUBBLE CRG, ESRF
(c) ESRF
(d) Institute of Crystallography, Moscow (Russia)
(e) University of Guelph, Guelph (Canada)