New numerical tools have been developed in the framework of a PhD thesis. These tools carried out, which have helped to improve our understanding of non-linear longitudinal beam dynamics in the presence of harmonic RF systems. Such systems are in operation on several low- and medium-energy machines in order to lengthen the bunches and thereby increase the Touschek lifetime. All the longitudinal issues have been addressed, such as transient beam loading with uneven fills, Robinson instabilities, Higher Order Modes (HOM) driven Longitudinal Coupled Bunch Instabilities (LCBI), as well as for high currents per bunch, the potential well and the microwave instability. Simulations have confirmed many experimental observations on various existing machines such as Landau damping of LCBI or strong phase transients with gaps in the fill pattern. They have also demonstrated the superiority of super conducting versus normal conducting harmonic cavities. This has very recently been confirmed by the commissioning of the superconducting Super3HC passive harmonic cavity at the Swiss Light Source. Taking into consideration all longitudinal effects, it transpires that an active superconducting third-harmonic cavity would constitute the only appropriate solution for the ESRF. It would be useful in single bunch and sixteen-bunch operation to improve the beam lifetime by a factor of 2 and 3, respectively.

Status of the Beam Loss Detection System

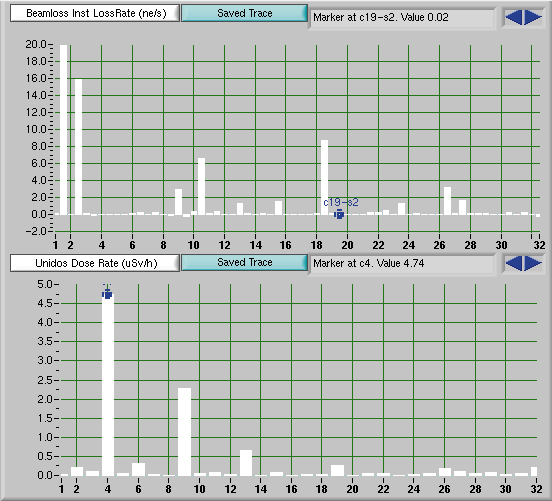
Monitoring and localising the electron beam losses has been a high priority over the last few years. Three networks of beam loss detectors are now in operation around the ring perimeter. Sixty-four neutron detectors are placed outside the shielding directly above each bending magnet. These detectors, which are part of the personnel safety system, give the most precise dose rates corresponding to the beam losses taking place during injection. However, due to their low sensitivity, they are not capable of monitoring the beam losses during a current decay. Two other networks of detectors based on ionisation chambers (Figure 137, lower graph) and glass scintillator coupled to a photomultiplier (upper graph) detect some shower residues generated by electron losses in every straight section of the storage ring. These detectors are extremely sensitive and allow, for example, the localisation of very small leaks or obstacles at an early stage when the induced losses are not yet sufficient to reduce the lifetime of the stored beam.

Fig. 137: Beam losses displayed along the ring's circumference (cells 1 to 32). The upper graph corresponds to the scintillator-photomultiplier detection. The lower one corresponds to the ionisation chamber type measurement.

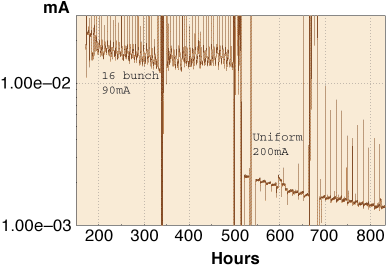
A new detector has been installed on the front-end of the ID6 beamline. Its role is to detect the amount of Bremsstrahlung passing down the beamline due to collisions between the electrons in the beam and the residual gas in the insertion device straight section. This diagnostic tool gives a relative measurement of the gas pressure integrated along the beam path in the small section ID vacuum chambers. It allows the monitoring of the vacuum conditioning of newly installed ID chambers and is non-destructive, allowing the measurement of the efficiency of the Non Evaporable Getter coating. Figure 138 shows the monitoring of Bremsstrahlung on ID6 normalised to the square of the current for a newly installed ID chamber. The sharp peaks correspond to high losses during injection. The higher losses in 16-bunch mode originate from the higher desorption induced by the high temperature of the chamber. In 200 mA uniform-filling mode, the signal decays with time following the reduction of desorption (vacuum conditioning).

 


Fig. 138: Normalised gas pressure in ID6 chamber taken by dividing the Bremsstrahlung count rate by the current squared.

A New Tune Monitoring System for the Booster

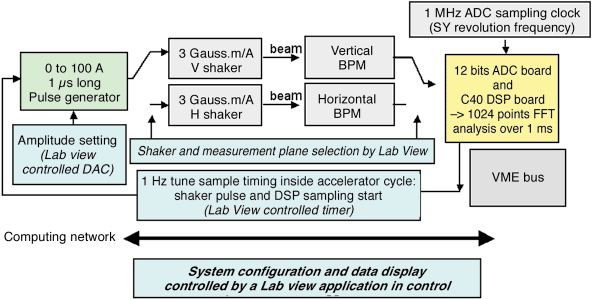
The booster tune monitor is a diagnostic tool used to measure the vertical and horizontal transverse resonant frequencies (or betatron tunes) of the electron beam accelerated in the booster. The beam is accelerated from 200 MeV to 6 GeV in 50 ms. To ensure optimum performance of the booster, the tunes must be kept constant during the acceleration cycle. To measure the tune, the beam is transversely excited by a 100A-1ms current pulse applied to the beam using a magnetic shaker. The beam position is recorded over 1024 turns (1ms). A FFT of the signal is performed on a DSP board and the resonant frequency is identified. The layout of this diagnostic is shown in Figure 139.

Fig. 139: Layout of the booster tune monitoring system.

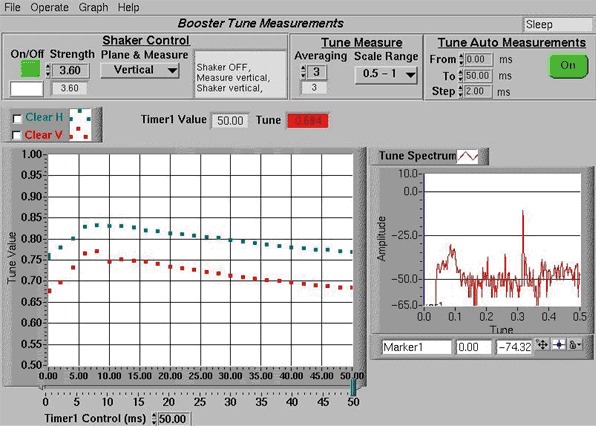
The front panel of the Labview application controlling the shaker and displaying the tunes is shown in Figure 140. This application now allows an automatic acquisition of the tunes throughout the acceleration cycle, making the booster tuning much easier.

Fig. 140: Control panel of the Booster tune monitor. The left hand side gives the horizontal and vertical tunes as measured along the 50 ms ramping time. The right hand side shows the FFT of the signal measured on the beam position monitor.

Progress in the Evaluation of the Longitudinal and Transverse Machine Impedance

The installation of more and more chambers of irregular shape in the machine, in particular transitions to vessels of small vertical aperture, has detrimental effects on the beam. The consequences of these irregularities and lack of electrical conductance of the vacuum chamber are multiple. The tunes vary with the current (detuning), which complicates the single bunch operation and limits the current. Transverse instabilities are triggered above some current thresholds [1], which can be cured by increasing the chromaticity at the cost of a reduction in lifetime. The underlying effect is characterised by a deformation of the self-field of the beam (wake field). The effect is formally expressed in the quantities known as longitudinal and transverse machine impedance.

As the impedance of the vacuum chamber components is very difficult to measure, the wake field generated by each chamber has to be calculated in three dimensions with a dedicated computer algorithm [2]. These computations use a lot of resources (cpu time and memory), which push present-day computers to the limit. This task was started in 2000 [3] and is still progressing. In 2002 further critical elements were identified, in particular the gap between the flanges, which provides a large contribution to the total impedance. More than half of the vertical detuning (vertical tune variation vs current) can now be accounted for. The transverse impedance can be expanded in the frequency space and typically presents a broad peak at certain high frequencies (broad resonator model). The numerically derived impedance in the frequency space shows such a peak at a much lower frequency than the model used so far which was fitted from various tune measurements [4]. It has become clear that the important vertical detuning observed on the ESRF storage ring is a consequence of the large number of discontinuities generated by the RF fingers located on both sides of the dipole chamber where the vertical beta functions are large. The transition to the narrow aperture insertion device chambers is less important than originally expected due to the low vertical beta function present there. As the evaluation of the transverse impedance budget in the vertical plane is now well advanced, its evaluation in the horizontal plane has just started. The flat nature of the ID chamber results in the presence of coherent and incoherent tune shifts which, in the horizontal plane, compensate each other for the fundamental head-tail mode (m = 0). This has been understood only recently and explains the very low horizontal detuning experimentally observed both in single bunch and multibunch. Nevertheless, following the recent installation of a large number of narrow gap chambers, a significant reduction of the current threshold of horizontal instability has been observed while such an effect was expected in the vertical plane instead. This is now better understood due to the very large horizontal beta functions in the even ID vessels and the horizontal impedance contribution.

References
[1] J.L. Revol, R. Nagaoka, P. Kernel, L. Tosi, E. Karantzoulis, EPAC 2000 Vienna.
[2] W. Bruns, GdfidL: A Finite Difference Programme with Reduced Memory and CPU Usage, PAC 97, Vancouver, p. 2651.
[3] ESRF Highlights 2000.
[4] T.F. Günzel, Evaluation of the vertical transverse impedance of the ESRF machine, EPAC 2002, Paris.