- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Electronic structure and magnetism
- Magnetic field induced orbital polarisation in cubic YbInNi4
Magnetic field induced orbital polarisation in cubic YbInNi4
In many cerium and ytterbium based heavy fermion materials the localised 4f electrons interact with conduction electrons giving rise to extraordinary low energy properties. Therefore, for a deeper understanding of these properties, the knowledge of the 4f ground-state wave functions is crucial.
In a crystalline environment the 4f electrons experience a crystal field which lifts the degeneracy of the Hund’s rule ground state and the resulting states are highly anisotropic. We used linear polarised soft X-ray absorption spectroscopy (XAS) at the rare earth M edges as a complementary tool to neutron scattering to determine crystal field ground-state wave functions in some tetragonal and orthorhombic cerium compounds [1-3]. Here the selection rules of the linear polarised light give the sensitivity to the initial state symmetry. However, XAS is a dipole technique, so that anisotropies in an environment with a higher than twofold rotational axis appear isotropic although they are not. Hence linear polarised XAS seemingly cannot be applied for cubic systems. Using the example of YbInNi4 where the crystal field ground state had been disputed in the past, we demonstrated that XAS with the application of a magnetic field induces linear dichroism even in cubic compounds, so that key information about the ground-state wave function can be obtained.
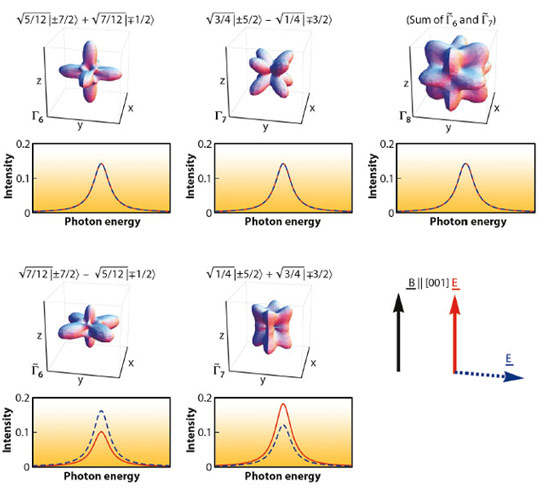
In the cubic symmetry of YbInNi4 the eightfold degenerate Hund’s rule ground state of Yb3+ with J = 7/2 splits into two doublets Γ6 and Γ7, and one quartet Γ8. These wave functions can be written in the basis of Jz
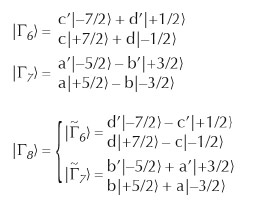 |
with a²+b²= a’²+b’² = c²+d² = c’²+d’² = 1. The upper panel of Figure 93 shows the corresponding angular hole-distributions. Despite the strong asymmetry, they would not show any linear dichroism in an XAS experiment because of the dipole limitations. This is also demonstrated in Figure 93 where the 3d  4f XAS spectra for the Γ6, Γ7 and Γ8 states have been calculated in a full multiplet routine [4] for the electric field vector E parallel (red) or perpendicular (blue dashed) to the [001] crystallographic axis. However, when lifting the remaining degeneracy with a magnetic field this changes considerably for some of the states: While the linear dichroism of the two Zeeman states of the Γ6 and Γ7 remains zero because they are Kramer’s doublets, this is not the case for the Γ8. The Γ8 quartet splits into two Zeeman-split
4f XAS spectra for the Γ6, Γ7 and Γ8 states have been calculated in a full multiplet routine [4] for the electric field vector E parallel (red) or perpendicular (blue dashed) to the [001] crystallographic axis. However, when lifting the remaining degeneracy with a magnetic field this changes considerably for some of the states: While the linear dichroism of the two Zeeman states of the Γ6 and Γ7 remains zero because they are Kramer’s doublets, this is not the case for the Γ8. The Γ8 quartet splits into two Zeeman-split  6 and
6 and 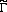 7 doublets and each of these two couples exhibits linear dichroism. The dichroism will only cancel out in the degenerate case. This can be understood when looking at the spatial hole-distribution of the
7 doublets and each of these two couples exhibits linear dichroism. The dichroism will only cancel out in the degenerate case. This can be understood when looking at the spatial hole-distribution of the 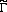 6 and
6 and 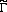 7 and Kramer’s doublets, which make up the Γ8 state (bottom panel of Figure 93). They do not have a fourfold rotational symmetry and consequently their anisotropy is observable in a dipole limited experiment. We call this effect magnetic field induced linear dichroism (MILD).
7 and Kramer’s doublets, which make up the Γ8 state (bottom panel of Figure 93). They do not have a fourfold rotational symmetry and consequently their anisotropy is observable in a dipole limited experiment. We call this effect magnetic field induced linear dichroism (MILD).
Yet, if the crystal field splittings are of the order of the Zeeman splitting, the magnetic field will cause Jz intermixing of the Γ6 and 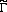 6 and the Γ7 and
6 and the Γ7 and 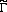 7 states, so that all states give rise to dichroism and a quantitative analysis taking into account the exact thermal population of each state becomes indispensable. Low and well-controlled temperatures are a prerequisite for such an experiment. Experimentally, this MILD idea could be realised at ID08, where a magnetic field can be applied perpendicular to the pointing vector of the light and an accurately calibrated temperature of 6.5 ± 0.5 K at the sample was provided.
7 states, so that all states give rise to dichroism and a quantitative analysis taking into account the exact thermal population of each state becomes indispensable. Low and well-controlled temperatures are a prerequisite for such an experiment. Experimentally, this MILD idea could be realised at ID08, where a magnetic field can be applied perpendicular to the pointing vector of the light and an accurately calibrated temperature of 6.5 ± 0.5 K at the sample was provided.
 |
|
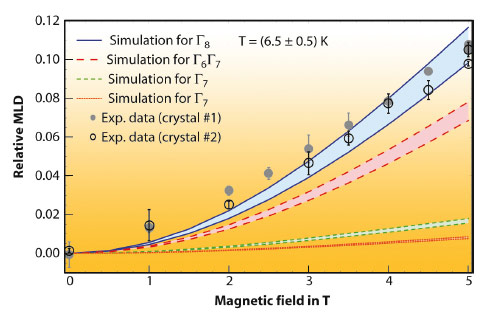
Fig. 94: MILD as function of field. The four different colours represent simulations corresponding to four different proposed crystal field scenarios. Open and closed circles are the measured MILD of YbInNi4. |
The four coloured regions in Figure 94 display the calculated MILD for four different proposed crystal field scenarios of YbInNi4. The upper limit of each region corresponds to 6 K and the lower one to 7 K. At large fields the MILD of the respective scenarios is well separated. These calculations can now be compared with the experimental MILD at 6.5 ± 0.5K shown as open and full circles in Figure 94, referring to measurements of two different crystals. Only the Γ8 quartet scenario fits well to the experimental data thereby unambiguously answering the question about the crystal field ground state.
Principal publication and authors
T. Willers (a), J.C. Cezar (b), N.B. Brookes (b), Z. Hu (c), F. Strigari (a), P. Körner (a), N. Hollmann (c), D. Schmitz (d), A. Bianchi (e), Z. Fisk (f), A. Tanaka (g), L.H. Tjeng (c) and A. Severing (a), Phys. Rev. Lett. 107, 236402 (2011).
(a) Institute of Physics II, University of Cologne (Germany)
(b) ESRF
(c) MPI for Chemical Physics of Solids, Dresden (Germany)
(d) Helmholtz-Center Berlin for Materials and Energy (Germany)
(e) Département de Physique, Université de Montréal (Canada)
(f) University of California, Irvine (USA)
(g) Department of Quantum Matter, ADSM Hiroshima University (Japan)
References
[1] P. Hansmann et al., Phys. Rev. Lett. 100, 066405 (2008).
[2] T. Willers et al., PRB 80, 115106 (2009).
[3] F. Strigari et al., PRB 86, 081105 (2012).
[4] A. Tanaka and T. Jo, J. Phys. Soc. Jpn. 63, 2788 (1994).