- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2002
- Materials Science
- Direct Evidence of Lattice-relaxed Charge-transfer Exciton-string
Direct Evidence of Lattice-relaxed Charge-transfer Exciton-string
Many novel low-dimensional electronic materials exhibit a high tunability between competing ground states. Interactions between charge, spin and lattice degrees of freedom are enhanced in the low-dimensional systems and cause cooperative phenomena and broken symmetries. The structure-function relationships are thus determined by self-trapped non-linear excitations. Besides well-known examples such as high-Tc superconductors, manganite oxide perovskites, conducting polymers or mixed-valence chains, the mixed-stack charge-transfer (CT) organic compounds undergoing neutral-ionic (N-I) transition appear as other promising materials and can serve as a model system to study the physics of non-linear excitations. In those quasi one-dimensional systems, the alternation of electron donor (D) and acceptor (A) molecules along stacks gives rise to chain multistability between a regular neutral (N) state ...D0 A0 D0 A0... and dimerised polar ionic states ... (D+A) (D+A)... This unusual electronic-structural transition is governed by the formation of CT exciton-strings, theoretically discussed by Nagaosa [1]. A chain is then inhomogeneous with the formation of lattice-relaxed CT (LR-CT) strings, sequences of I dimers within a N chain:
...A0 D0 A0 (D+A) (D+A) (D+A) (D+A) D0 A0 D0...
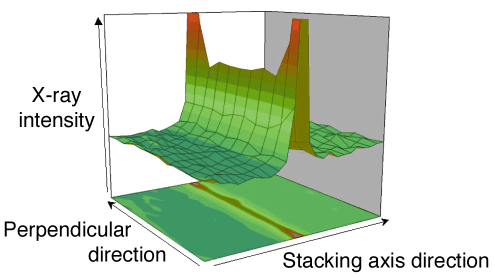
New physical properties originate from these non-linear excitations, such as photo-induced phase transformations, a new type of ferroelectric phenomena or negative resistance effects. The excitation of CT exciton-strings has been observed by optical spectroscopy [2]. However, direct evidence of their lattice-relaxed state, which may be thermally activated, had not been found. Here we report on such a fundamental observation by X-ray diffuse scattering in different CT complexes. The size and concentration of these LR-CT strings have been determined by diffuse scattering measurements taking advantage of the X-ray flux and high resolution at BM2, the D2AM CRG beamline. The LR-CT exciton-strings extending along the stacking axis a are directly evidenced by diffuse (b*,c*) planes as shown in Figure 87. Scans in reciprocal space makes it possible to extract precisely the intrinsic correlation lengths which characterise the mean size of these fluctuating nanodomains, and from the intensity at maximum (IM), the temperature evolution of susceptibility. The results obtained for a compound presenting a continuous phase transition are plotted in Figure 88.
 |
|
Fig. 87: Diffuse plane perpendicular to the stack showing the 1D nature of the fluctuating CT nanodomains. |
 |
|
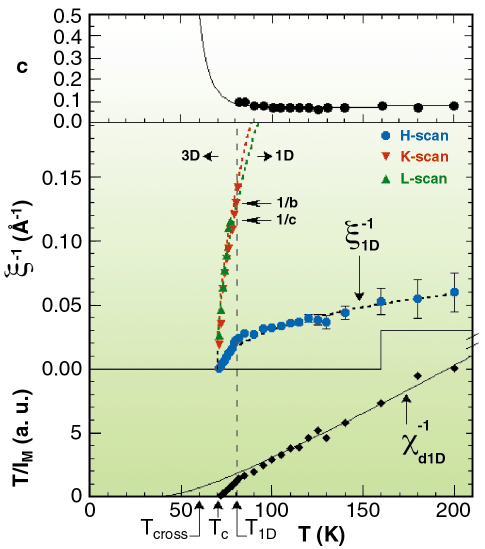
Fig. 88: High-resolution measurements of the inverse X-ray intensity T/IM (squares, bottom), inverse correlation lengths (middle) along a*(blue), b*(red) and c*(green), and concentration in I species c (dots, top). Tc is the phase transition temperature and T1D is the lower limit of 1D fluctuations. The dotted lines (bottom) represents the 1D susceptibility, while the dashed lines for the transverse correlations (middle) correspond to the mean field approach for weakly coupled chains. |
The almost equal perpendicular correlation lengths 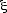 b* and
b* and 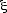 c* reach the inter-stack distances at TID, 10 K above the 3D phase transition. At the same temperature, anomalies of the intra-chain correlation length,
c* reach the inter-stack distances at TID, 10 K above the 3D phase transition. At the same temperature, anomalies of the intra-chain correlation length,  a*, and of the susceptibility are observed. This clearly indicates a crossover from a 3D to a pronounced 1D regime for the fluctuations. The important cooperativity inside the stack is reflected in the size of the strings extending around 100 Å at TID, giving direct evidence of 1D LR-CT fluctuations. The comparison of IM and
a*, and of the susceptibility are observed. This clearly indicates a crossover from a 3D to a pronounced 1D regime for the fluctuations. The important cooperativity inside the stack is reflected in the size of the strings extending around 100 Å at TID, giving direct evidence of 1D LR-CT fluctuations. The comparison of IM and  a* makes it possible to deduce the concentration of thermally-activated excitations (Figure 88). Another aspect of these systems is that the size and also the concentration of these nanoscale non-linear excitations can be triggered by pressure, temperature or light irradiation.
a* makes it possible to deduce the concentration of thermally-activated excitations (Figure 88). Another aspect of these systems is that the size and also the concentration of these nanoscale non-linear excitations can be triggered by pressure, temperature or light irradiation.
This kind of investigation, actually pursued to understand the photo-induced and quantum fluctuation effects, is fundamental with regards to the universality of the equilibrium and out of equilibrium multi-scale phenomena in these novel low-dimensional electronic materials.
References
[1] N. Nagaosa, J. Phys. Soc. Jap. 55, 3488 (1986).
[2] M. Kuwata-Gonokami et al, Nature 367, 47 (1994).
Principal Publication and Authors
E. Collet (a), M.H. Lemée-Cailleau (a), M. Buron (a), H. Cailleau (a), S. Ravy (b), T. Luty (c) J.F. Bérar (d), P. Czarnecki (e), and N. Karl (f), Europhys. Lett. 57, 67-73 (2002).
(a) Groupe Matière Condensée et Matériaux, Université de Rennes1 (France)
(b) Laboratoire de Physique des Solides, Université Paris-sud, Orsay (France)
(c) Institute of Physical and Theoretical Chemistry, Wroclaw (Poland)
(d) D2AM CRG, ESRF
(e) Institute of Physics, Adam Mickiewicz University, Poznan (Poland)
(f) Physikalisches Institut, Universitat Stuttgart (Germany)



