- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- X-ray Absorption and Magnetic Scattering
- E1-E2 X-ray Resonant Scattering
E1-E2 X-ray Resonant Scattering
Near-edge X-ray absorption (and particularly its dichroism) and X-ray scattering are powerful techniques in the study of the microscopic properties of matter.
Until a few years ago, experimental investigations and theoretical treatments have mainly focussed on resonant processes involving pure E1 (electric dipole) and E2 (electric quadrupole) transitions between core levels and empty valence states. Only recently Goulon and his collaborators [1] have pointed out the importance of the study of resonant absorption processes induced by the E1-E2 interference. They have observed three new effects, termed respectively X-ray natural, nonreciprocal and magnetochiral dichroism. In each case the inner-shell excitation is controlled by the E1-E2 interference. Observing a non-vanishing signal thus requires an ordered structure and the breaking of space inversion symmetry.
A theoretical interpretation of these effects has been given by Carra et al. [2]; it relates the observed spectra to microscopic polar and magnetoelectric properties of the sample.
The importance of E1-E2 processes in resonant X-ray scattering has emerged from experiments of Templeton and Templeton [3] and numerical calculations by Elfimov et al. [4]. A description of these effects, which requires an analytical study of the properties of the fE1-E2 scattering amplitude, has been given by the ESRF theory group; working within an atomic model and using a spherical tensor representation, it has been shown that fE1-E2 can be written as a linear combination of pairs of irreducible tensors of increasing rank K = 1,2,3. Each pair is given by the scalar product between a geometrical factor (dependent on light polarisation and wave vector) and the ground-state expectation value of an effective one-electron operator (order parameter) obtainable from the orbital and spin angular momentum L and S, the electric dipole n = r/r and from the magnetoelectric tensors ![]() L = (Lxn-nxL)/2 and
L = (Lxn-nxL)/2 and ![]() S = (nxS).
S = (nxS).
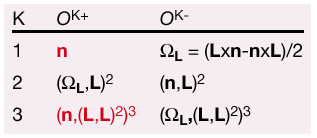
In particular, it has been shown that the spin-independent scattering amplitude describing excitations at the K-edge can be written as a linear combination of three orbital polar (OK+) and three orbital magnetoelectric (OK-) order parameters (the operators OK+ and OK-, for K = 1,2,3 are listed in Table 2. Notice that the operators depicted in red cannot be detected by X-ray absorption experiments, as their angular dependence vanishes in the forward direction). The order parameters (OK±) can be independently measured by selecting appropriate experimental conditions.
 |
|
Table 2: Spinless order parameters. |
The presence of O1+ = n in the resonance-scattering amplitude indicates the possibility of observing ferroelectric and antiferroelectric Bragg peaks using X-ray resonant scattering.
Ferroelectric reflections could be observed, for instance, near the Ti K-edge (~ 4966 eV) in barium titanate by selecting the ![]()
![]()
![]() channel (e.g.
channel (e.g. ![]() f =
f = ![]() 0 =
0 = ![]()
![]() where
where ![]() f and
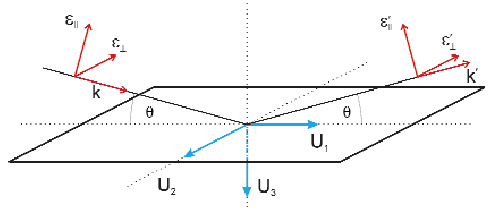
f and ![]() 0 are the polarisations of the outgoing and incoming photon; for the definition and notation adopted see Figure 126) when the quantisation axis z is such that U2.
0 are the polarisations of the outgoing and incoming photon; for the definition and notation adopted see Figure 126) when the quantisation axis z is such that U2.![]() = ±1/
= ±1/![]() 5.
5.
 |
|
Fig. 126: Scattering geometry. The basis U1, U2 and U3 are respectively given by: U1 = ( |
In summary, our theoretical studies of the excitation mechanism involving non-pure transitions as E1-E2, open up new possibilities for the investigation of the electronic properties in noncentrosymmetric crystals using X-ray absorption and resonant scattering. The results obtained indicate the possibility of detecting Bragg peaks from ferroelectric, antiferroelectric and magnetoelectric crystals using X-rays at resonance.
References
[1] J. Goulon, A. Rogalev, F. Wilhelm, C. GoulonGinet, P. Carra, D. Cabaret, and C. Brouder, Phys. Rev. Lett. 88, 237401 (2002), and references therein.
[2] P. Carra, A. Jerez and I. Marri Phys. Rev. B 67, 045111 (2003).
[3] D. H. Templeton and L.H. Templeton, Phys. Rev B 49, 14850 (1994).
[4] I.S. Elfimov, N.A. Skorikov, V.I. Anisimov and G.A. Sawatzky, Phys. Rev. Lett. 88, 015504 (2002); 88, 239904 (E) (2002).
Principal Publication and Authors
I. Marri (a) and P. Carra (b), in print Phys. Rev. B 69 (2004).
(a) S3 and INFM, Università degli Studi di Modena e Reggio Emilia (Italy)
(b) ESRF



