- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2017
- X-ray nanoprobe
- Revealing the principles of morphogenesis of glass spicules in marine sponges from the class Demospongiae
Revealing the principles of morphogenesis of glass spicules in marine sponges from the class Demospongiae
Demospongiae is a class of marine sponges that use amorphous glass structures, in the form of highly regular 3D microscopic spicules, to mechanically enhance their body, though the physical principles behind spicule formation had remained unknown. A model that describes the principles of spiculogenesis has been proposed.
Microscopic silica elements called spicules (< 1 mm) are a paradigm example of symmetry in biological systems. Some of the most common examples include needle-like spicules in the shape of a simple glass fibre, tripod-like spicules with glass branches radiating from a common centre in strictly defined angles, and spicules with branches radiating in numerous random directions forming a sphere-like morphology. Each branch of a spicule contains an organic axial filament that passes through its centre. These filaments are made of enzymatically active proteins named silicateins that are responsible for silica biomineralisation and also act as a template for its deposition [1]. So far, the mechanisms responsible for the morphogenesis and the high regularity of the filament itself have remained unknown.
The proteins inside the axial filament are arranged in a perfectly regular mesoscopic crystalline structure [2] that was thought to extend through the entire spicule. It was therefore hypothesised that the highly regular shape of the filament and its branching behaviour are linked to the crystalline properties of the protein assembly. It was suggested that branching occurs on specific crystallographic planes of the protein lattice, resulting in remarkably symmetric spicule morphologies and very specific branching angles.
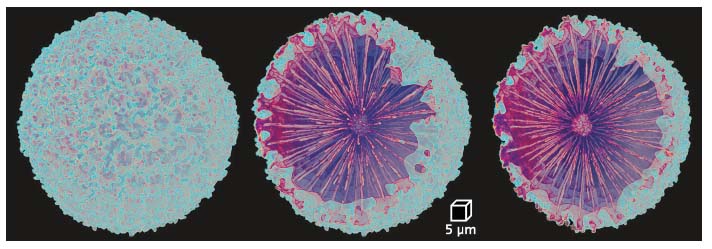
To corroborate this hypothesis, three types of spicules with increasing levels of spatial complexity, taken from three different sponges, were analysed: needle-shaped spicules from the sponge Tethya aurantium, tetrapod-like spicules from the sponge Stryphnus ponderosus (three branches radiating from the main shaft, each splitting into two additional branches) and sphere-like spicules from Geodia cydonium. To correlate between the crystalline properties of the axial filaments and their spatial distribution, the properties of the protein lattice of the axial filament and its spatial morphology in the three spicules were studied. Diffraction data, obtained at beamline ID13, showed that the proteins in all three spicules have a hexagonal packing with lattice parameters of a ≈ 6 nm and c ≈ 12 nm. The spatial distribution of the filament was studied using nano-tomography at ID16A, in the case of Geodia cydonium (Figure 80), and micro-tomography at ID19, in the case of Tethya aurantium and Stryphnus ponderosus.
 |
|
Fig. 80: 3D tomographic reconstruction of a sphere-like spicule from the sponge Geodia cydonium. |
The results demonstrate the capacity of the organism to create different templates for glass deposition by forming a variety of three-dimensionally organised filaments, using a common hexagonal unit of the protein crystal. This observation is analogous to a man-made approach to technologically relevant nanocrystalline structures [3], such as rod-like, branched and hyperbranched crystals. In these structures, the branching occurs on specific crystallographic planes of the atomic lattice and the final morphology depends on growth conditions. It is asserted that the same principles apply for the morphogenesis of the axial filaments.
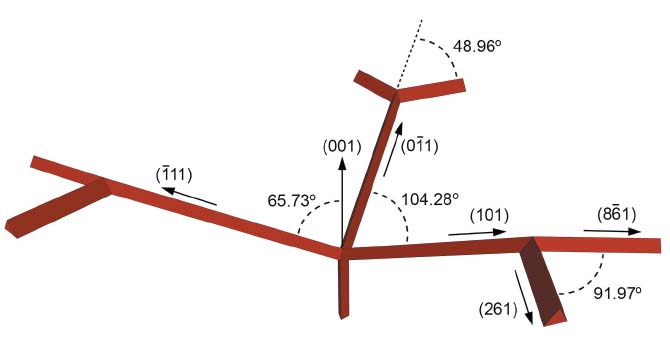
On the basis of this analogy, the X-ray crystallographic data, and the branching angles extracted from tomographic reconstructions, a model that describes the crystallographic directions in which spiculogenesis proceeds has been proposed. The filament in the needle-like spicule from T. aurantium shows no branching, which results in a needle-like morphology of the spicule. The sphere-like spicule from G. cydonium is hyperbranched, developing a sphere-like morphology. At the same time, the axial filament in the tripod from S. ponderosus shows a perfect threefold symmetry. On the basis of the known lattice parameters, it was possible to estimate the possible angles between the different arms of the spicules by assuming that the branching occurred on a specific crystallographic plane. By comparing the theoretical angle to the ones measured using the tomography data, the exact planes on which the branching proceeded was determined. For example, the angle between the main shaft (direction [001]) and the three main branches, assuming that the branching occurred on [101]-planes was calculated as 65.73°, which is close to the mean value of 66.0° ± 2.0°, measured in the spicule. The final model is summarised in Figure 81.
 |
|
Fig. 81: 3D model of the axial filament in the spicule from Stryphnus ponderosus and the Miller indices of the leading crystallographic planes in the branches. |
To conclude, it is astonishing that both nature and humankind converged to a similar thermodynamically driven fabrication method independently. The complexity and the high symmetry of glass architectures found in marine sponges, and the elegance with which they are formed by a living tissue, provides exciting future research opportunities.
Principal publication and authors
Shaping highly regular glass architectures: A lesson from nature, V. Schoeppler (a), E. Reich (a), J. Vacelet (b), M. Rosenthal (c), A. Pacureanu (c), A. Rack (c), P. Zaslansky (d), E. Zolotoyabko (e) and I. Zlotnikov (a), Sci. Adv. 3, eaao2047 (2017); doi: 10.1126/sciadv.aao2047.
(a) B CUBE–Center for Molecular Bioengineering, Technische Universität Dresden (Germany)
(b) IMBE, CNRS, Aix-Marseille Université, Université d’Avignon, IRD, Station Marine d’Endoume, Marseille (France)
(c) ESRF
(d) Julius Wolff Institute for Biomechanics and Musculoskeletal Regeneration, Berlin, (Germany)
(e) Department of Materials Science and Engineering, Technion, Haifa (Israel)
References
[1] M.-J. Uriz, Can. J. Zool. 84, 322-356 (2006).
[2] I. Zlotnikov et al., Adv. Mater. 26, 1682-1687 (2014).
[3] H. Li et al., Acc. Chem. Res. 46, 1387-1396 (2013).



