- Home
- News
- Spotlight on Science
- In situ dynamic-mechanical...
In situ dynamic-mechanical analysis and SAXS studies of silica-rubber composites
15-06-2020
Nano-composite materials can be tailored to suit many applications through their hierarchical structures spanning many length scales. In situ experiments at beamline ID02 provide an understanding of the microscopic deformation characteristics of silica-rubber composites.
Nanofillers within elastomers are known to form hierarchical structures, varying from single particles to clusters of the order of several nm up to microscopic agglomerates in the range of several μm. As a consequence of this, nano-composite materials exhibit strongly-improved dynamic-mechanical properties and their most prominent application is in car tires. In situ small-angle scattering methods are ideal probes of the material in order to reveal the correlation between the filler structure and the associated macroscopic dynamic properties of composites.
For this purpose, a versatile modular stretch-rheometer was built consisting of a mechanical unit and a sample chamber. An exchangeable force transducer of up to 50 or 500 N in tension and compression allows in situ or ex situ uniaxial testing. The installation of such a device into the X-ray beam, in combination with the high resolution of beamline ID02, allows unique parallel investigations of structural and mechanical properties. This device, operated in situ, allows the evolution of nanofilled elastomers during a uniaxial deformation to be followed by the detection of the scattering pattern. Stress-strain curves can be recorded at the same time.
The scattering function of silica-filled styrene-butadiene random copolymer rubbers (SBR) under a continuous uniaxial strain cycle was investigated using ultra-small-angle X-ray scattering (USAXS) at beamline ID02. The microscopic hierarchical arrangement of aggregating nanofiller particles in the rubber matrix was determined at different strain stages from the quiescent state up to a 100% increase in the initial sample length using a slow cross-head speed of 0.2 mm/s and subsequent unloading. The 2D-scattering patterns were collected every 30 s during 0.01 s corresponding to a deformation step of about 2% in order to follow the evolution of the structure with the deformation. The 2D scattering patterns yield instantaneous information about the size and distribution of clusters formed by primary particles and relate ideally to the particular stress in the elastomers.
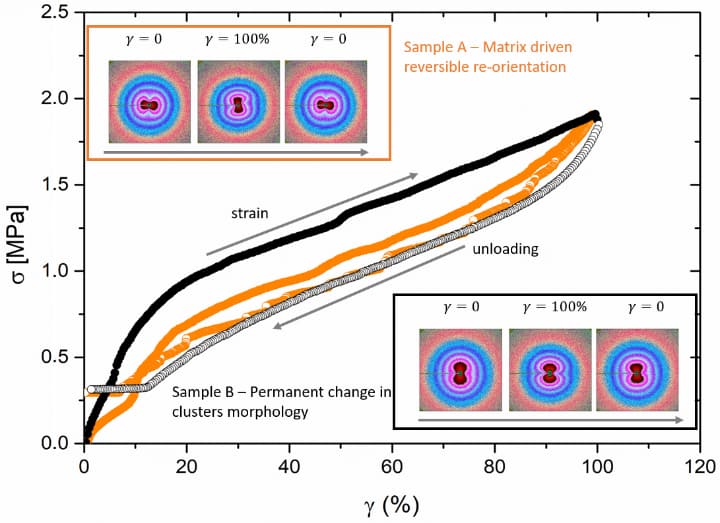
The scattering of the filled rubbers with silica (90 phr 1165 MP, Solvay) was found to be already anisotropic as a consequence of the milling and vulcanisation steps. Different 2D patterns were identified as butterfly shapes and were related to different preferential orientations of the clusters within the same sample. The present study correlates the initial preferential filler orientation to the quasi-static deformation along the principal axis of the strain tensor. As an example, two different and perpendicular initial states are presented in Figure 1 (identified as A and B).
 |
|
Figure 1. Correlation between scattering pattern evolution and stress-strain curves for two different initial orientations. Coloured lines correspond to the coloured legends. |
A fractal scattering model was developed to allow polydispersity in the primary particles, which are characterised by a fractal or rough surface. The application of this to sector-binned intensities along the principal deformation axis leads to the quantitative identification of the structure of the average clusters with which correlations between the morphology and the simultaneously-recorded stress-strain properties of the composite system are reached.
The two examples shown in Figure 1 illustrate different evolutions of the cluster parameters detected by non-linear fitting of the scattering intensities. In the case of A, due to the initial orientation of the clusters in a direction perpendicular to the deformation axis, the strain field in the matrix promotes a re-orientation of primary particles inside the clusters. The number of particles remains roughly constant. The dependence of the cluster with the strain seems to be coherent with the matrix deformation. The effect is completely reversible upon unloading. In the second case B, where the clusters are initially oriented along the deformation direction, the macroscopic deformation seems instead to induce a permanent change of the morphology of the clusters.
As illustrated by Figure 1, a full agreement between the structural evolution and the mechanical behaviour of the two different cases was observed.
These differently-oriented clusters respond in a different way to the applied deformation coherently with the scattering pattern evolution. The Mullins effect, which is associated to the hysteresis loop of the mechanical curves, concerns mainly the filler-rubber coupling with the rubber network and is found to be more evident in the case B where an initial orientation of the anisotropic pattern along the deformation direction is reported. The area of the hysteresis loop is directly proportional to the dissipation, i.e. loss of elasticity in the up-down strain cycle. The thinner loop in case A is due to the pronounced reversibility of the changes imposed by the strain to the initial average orientation in the opposite direction, indicating an enhanced elasticity and more reinforcing properties compared to B.
This work was financed by the FNR Luxembourg in collaboration with Goodyear S.A., Colmar-Berg, Luxembourg.
Principal publication and authors
Hierarchical scattering function for silica-filled rubbers under deformation: effect of the initial cluster distribution, M. Staropoli (a), D. Gerstner (b), M. Sztucki (c), G. Vehres (d), B. Duez (b), S.Westermann (b), D. Lenoble (a), W. Pyckhout-Hintzen (d), Macromolecules, 52, 9735-9745 (2019); doi: 10.1021/acs.macromol.9b01751.
(a) Luxembourg Institute of Science and Technology, Belvaux (Luxembourg)
(b) Goodyear S.A, Colmar-Berg (Luxembourg)
(c) ESRF
(d) Forschungszentrum Jülich (Germany)



