- Home
- News
- Spotlight on Science
- Magnetic refrigeration:...
Magnetic refrigeration: unusual interplay between magnetism and chemical bonding revealed
11-10-2016
Magnetic refrigeration is based on the magnetocaloric effect, which is associated with the temperature change of a material when placed in a magnetic field. X-ray techniques and DFT calculations were used to investigate the first-order magnetoelastic transitions of Fe2P-based materials. The electron density was studied across the transition and a distinct charge redistribution around the Fe atoms at the ferromagnetic transition was found for the paramagnetic state which deforms the unit cell. DFT calculations show a simultaneous decrease in the magnetic moment of Fe, indicating that there is competition between the magnetic moment and covalent bonding.
The giant magnetocaloric effect makes cooling based on magnetic refrigerants a viable option. A first-order magnetoelastic transition is at the origin of this effect and it is characterised by an isothermal entropy change and adiabatic temperature change that results from a change in applied magnetic field. Under adiabatic conditions, a decrease in magnetic entropy due to moment alignment parallel to a magnetic field is compensated by an increase in lattice entropy, leading to a temperature increase in the material.
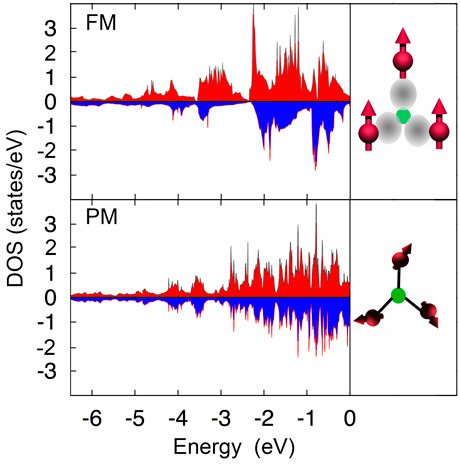
Previous density functional theory (DFT) calculations predict a distinct change in electronic structure and magnetic moments across the magneto-elastic transition in Fe2P-based materials [1]. In particular, Fe atoms on the 3f site display a partially quenched magnetic moment in the paramagnetic state. We therefore propose that competition between bond formation and moment formation takes place (Figure 1).
To verify this prediction, we used XAFS and XRD to study the electron density and compared it with DFT calculations [3]. The XAFS measurements were performed at beamline BM26 (DUBBLE) and the powder diffraction was performed at beamline BM01A (SNBL).
Figure 2 shows the change in the electron density of the ferromagnetic state compared to the paramagnetic state. In Figure 2a, the measured electron density difference between 150 K and 350 K is plotted. In Figure 2b and 2c, the corresponding results from first-principle DFT calculations are shown. In Figure 2b the Fe atoms are allowed to relax to the experimentally determined equilibrium position, while in Figure 2c the relative coordinates of the atoms were kept fixed.
The calculated electron density difference plot in Figure 2c shows that electrons shift from a dxz to a dz2 orbital when crossing the magnetoelastic transition from the paramagnetic to the ferromagnetic state, respectively. In Figure 2b one lobe of the dz2 orbital is obscured, and the two lobes of the dxz orbital on either side of the atom are not clearly defined due to the relative movement of the internal coordinate of Fe. The experimental result shows the same features as the calculated plot, indicating a redistribution of electron density. This implies that in the paramagnetic phase, a covalent bond is formed between Fe and the P/Si atoms, leading to a decrease in the a and b lattice parameters and an increase in the c lattice parameter. This can be understood from a magnetic and a chemical viewpoint. The Fe atoms only carry a sizable magnetic moment when the exchange interaction between the Mn layers is sufficiently strong. However, as the exchange interaction is overcome by magnetic fluctuations, we find that the ferromagnetic transition is associated with a remarkably strong reduction of the Fe magnetic moment. In other words, the ferromagnetic exchange field exerted by the Mn moments on the Fe positions stabilises the Fe magnetic moments, while as soon as it vanishes, the Fe valence electrons prefer to bond with neighbouring P/Si, which destabilises the moments.
The insight into the mechanism of first-order magneto-elastic phase transitions gained here makes the design of more efficient magnets for refrigeration possible.
Principal publication and authors
Efficient room-temperature cooling with magnets, M.F.J. Boeije (a), P. Roy (b), F. Guillou (a,c), H. Yibole (a), X.F. Miao (a), L. Caron (a,d), D. Banerjee (c), N.H. van Dijk (a), R.A. de Groot (b) and E. Brück (a), Chemistry of Materials 28, 4901−4905 (2016); doi: 10.1021/acs.chemmater.6b00518.
(a) Fundamental Aspects of Materials and Energy, Faculty of Applied Sciences, Delft University of Technology (The Netherlands)
(b) Electronic Structure of Materials, Faculty of Sciences, Radboud University, Nijmegen (The Netherlands)
(c) ESRF
(d) Max Planck Institute for Chemical Physics of Solids, Dresden (Germany)
References
[1] N.H. Dung, Z.Q. Ou, L. Caron, L. Zhang, D.T.C. Thanh, G.A. de Wijs, R.A. de Groot, K.H.J. Buschow, E. Brück, Adv. Energy Mater. 1, 1215−1219 (2011).