Small-angle scattering patterns from swollen networks depend sensitively on the details of how they are cross-linked. This is because the relevant chemical reactions connect topologically different regions, thus imprinting many different length scales on the system. When such a network is swollen, the random local elastic strains due to these cross-links give rise to density fluctuations that usually extend over a spatial range of several nanometres. If they are now stretched, such swollen networks yield small-angle scattering patterns whose iso-intensity contours exhibit a characteristic figure-of-eight (butterfly) pattern [1].

Networks are also formed when fillers are blended with a polymer. A commonly used filler is carbon black (CB), which consists of fractal aggregates (fractal dimension D < 2) of primary particles. When carbon black is blended into a polymer, a percolating network develops that connects aggregates in such a way that the resulting material is electrically conducting (e.g. CB in polyethylene for electrical components). The filler can also enhance the mechanical properties (e.g. CB in elastomers for automobile tyres). Mechanical and electrical properties of CB filled polymers depend not only on the volume fraction of the filler particles, but also on their structure and on their distribution, which lend themselves to investigation by ultra small-angle X-ray scattering (USAXS).

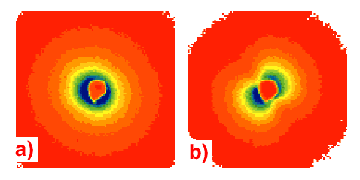Figure 43
Fig. 43: USAXS patterns from high-density polyethylene containing 30% vol carbon black prepared: a) by solution precipitation; b) by blending in the melt. (Limits of horizontal scale: - 4x10 -2 nm -1 to 4x10 -2 nm -1). 

USAXS measurements were carried out at BM2, the French CRG beamline D2AM. For the CB used (N330), percolation of aggregates occurs above about 10% by volume of CB. Depending on the blending method, the resulting scattering patterns can be inherently anisotropic. Figure 43a shows the scattering pattern obtained from a high-density polyethylene sample containing 30% CB by volume. This sample is isotropic and was prepared by precipitation from solution followed by moulding. The equivalent pattern from a similar sample prepared by direct blending in the melt is shown in Figure 43b; here, the butterfly figure reveals anisotropy on a length scale of about 100 nm, which persists after the moulding process. These figures show that a difference arises between the two carbon black networks in the degree of interpenetration among the aggregates; this difference is also reflected in their electrical properties. A second example (Figure 44) shows the effect of stretching a non-cross-linked elastomer (ethylene-propylene rubber, EPR) loaded with the same CB. At concentrations below the percolation threshold (Figure 44a,b), no anisotropy is observed, even under uniaxial stretching. Above the percolation threshold, however (Figure 44c,d), the results are highly sensitive to the degree of mutual interpenetration of the CB aggregates. The role of aggregate interpenetration (which is allowed because the fractal dimension is smaller than 2) in the mechanical behaviour of CB-polymer composites is clearly shown. These features, which are similar to those observed in swollen polymer networks, are fully consistent with models of reinforcement of rubber by fractal aggregates [2].

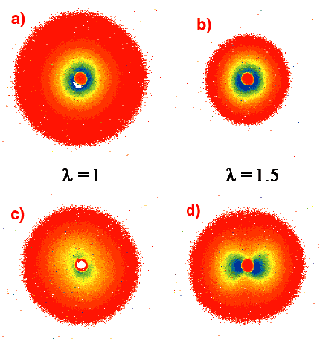Figure 44
Fig. 44: USAXS pattern from EPR-CB composite: below percolation threshold (5% vol) a) before and b) after stretching; above percolation threshold (20% vol) c) before and d) after stretching. (Limits of horizontal scale: - 9.5x10 -2 nm -1 to 9.5x10 -2 nm -1).

With the D2AM camera, as with standard Bonse-Hart devices, measurements of opaque samples can be made over the range of visible light scattering. Our observations with a 2-dimensional CCD detector have the advantage of being sensitive to anisotropy.

References
[1] R. Oeser, C. Picot and J. Herz in Polymer Motions in Dense Systems, ed. D. Richter and T. Springer, Springer, Proceedings in Physics 29, 104 (1987).
[2] T.A. Witten, M. Rubinstein and R.H. Colby, J. Phys. France, 3, 367 (1993).

Principal Publication and Authors
F. Ehrburger-Dolle (a,b), M. Hindermann-Bischoff (a), F. Livet (c), F. Bley (c), C. Rochas (b) and E. Geissler (b), to appear in Langmuir.
(a) ICSI CNRS, Mulhouse (France)
(b) LSP, UJF-CNRS, Grenoble (France)
(c) LTPCM, INPG, Grenoble (France)