In recent years, a vast variety of self-organised systems of 2D and even 1D nanocrystals were grown by heteroepitaxy. In almost all of these systems, materials with slightly different lattice parameter are grown epitaxially on top of each other. X-ray diffraction is the most appropriate tool for the characterisation of crystalline nanostructures. There are, however, difficulties in separating their structure and composition.

Here we introduce a method to overcome this problem via contrast variation using anomalous diffraction at the GaAs/InAs (200) reflection. As GaAs crystallises in the zinc-blend structure, the structure amplitude Fhkl for the (200) reflection is F200 = fGa ­ fAs, where fGa,As denote the scattered amplitude from the corresponding atom. The atomic scattering factor is a complex number that describes the scattering from an atom as a driven oscillator, taking into account the shift in phase, 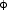phi_cap.gif (Phi Capital) , with respect to the exciting wave field. 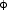is of importance close to an absorption edge, when electrons of a shell are in resonance, and scatter with a phase-shift.

It becomes clear that once the absolute values of the scattering factors and their phases are equal, the scattered amplitude is completely annihilated. |fGa| = |fAs| is fulfilled at the two energies, above and below the K-edge of As. The corresponding calculated intensity for the (200) reflection of GaAs and InAs is depicted in Figure 31.

Fig. 31: Calculated (200) intensity for GaAs (red line) and InAs (blue line).

To demonstrate and exploit the expected effect on the scattered intensity around the (200) surface reflection, a grazing incidence X-ray diffraction (GID) experiment was performed at beamline ID1. The sample consisted of a (001)-GaAs substrate covered with InAs dots grown by MBE in the Stranski-Krastanow growth mode. The two chosen energies, where E1 = 11.8 keV and E2 = 12.38 keV, are marked with an arrow in Figure 31. Radial scans along <100> through the (200) reflection, together with fits are presented in Figure 32. As expected, a tremendous change in the scattered intensity of the GaAs substrate is found, whereas the diffraction from the InAs quantum dots is less influenced.

Fig. 32: Radial scan through (200) InAs dot and GaAs substrate reflection at (a) 11.8 keV and (b) 12.38 keV. Red lines are simulations.

In order to fit the diffraction curves, we developed a model for the diffraction from coherently-grown InAs dots on a GaAs (001) substrate. The composition was allowed to vary with the height over the substrate from pure GaAs to GaXIn1­x with 0<x<1 and the condition of a monotonic decay of the gallium content with increasing height. Accordingly, the lattice parameter was allowed to relax monotonically from aGaAs towards aInAs. To exploit the fact that the Ga-containing parts of the dot change their scattering contribution at the two energies by a factor of 20, whereas the InAs intensity contribution changes only by a factor of 1.3, both scans were fitted simultaneously (red lines in Figure 32). The effect of the Ga interdiffusion into the dot causes a weakening of the scattering contribution from the dot material at 12.38 keV. Therefore the measured intensity is directly linked to this compositional change.

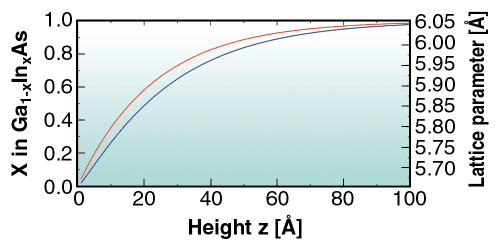
The resulting interdiffusion and lattice parameter profile as a function of the height z above the substrate surface is shown in Figure 33. The red line describes the decay of the Ga content inside the dots with the dot height whereas the blue line describes the change of the lattice parameter. The fact that these two parameters have a very similar behaviour indicates that the strain energy in this sample was minimised by interdiffusion.

Fig. 33: Material composition (left scale, red line) and lattice parameter in the dots (right scale, blue line) as a function of the height z resulting from the fits in Figure 32.

In summary, we wish to emphasise that contrast maximisation by anomalous diffraction on superstructure reflections is a powerful tool to enhance the scattering contribution from quantum dots on a substrate.

Principal publication and Authors
T.U. Schülli (a), M. Sztucki (a), V. Chamard (a), D. Schuh (b), T.H. Metzger (a), Appl. Phys. Lett. 81, 448 (2002).
(a) ESRF
(b) Walter Schottky Institut Technische Universität München, Garching (Germany)