Correlation spectroscopy with coherent X-rays (XPCS) is a speciality of beamline ID10A (TROÏKA) and it offers the interesting possibility to probe bulk dynamics as well as dynamic properties of surfaces. The surface application resides in the fact that when the X-ray beam is applied at an incidence angle i below c (the critical angle for total external reflection) a unique surface sensitivity is obtained. Moreover, multiple scattering effects can largely be ignored for X-rays and with the advent of fast avalanche photo-diode (APD) detectors it has become possible to quantify dynamic phenomena up to MHz frequencies. This shows that the gap to energy-domain techniques, especially neutron spin-echo (NSE) [1] has been bridged.

 

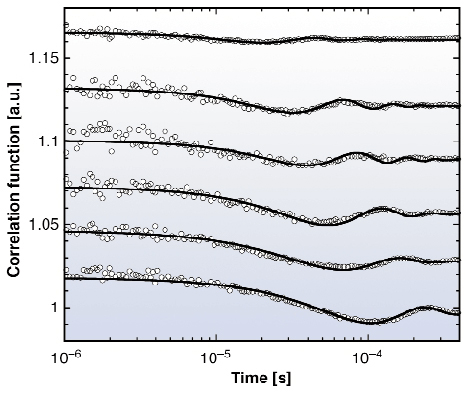
Fig. 71: Correlation functions taken at increasing exit angles c corresponding to an increase in momentum transfer q parallel to the surface (bottom to top). The data were taken on a water surface at T = 5°C with i < c and the oscillatory behaviour indicates the presence of propagating capillary waves. The q dependence of the propagation frequency p is clearly visible (dispersion) and follows p µ q3/2. The solid lines are fits assuming heterodyne mixing [2].

 

Recently, the first surface XPCS experiment employing heterodyne mixing was reported [2]. In the heterodyne mixing scheme, coherent interference between the scattered field (carrying the dynamic information) and a static reference field is evoked. Interference with a strong reference field amplifies the (weak) scattered signal while preserving the dynamic information. This leads to the presence of a heterodyne component in the time-correlation function of the scattered intensity. When capillary wave dynamics is quantified by XPCS performed under grazing incidence conditions, the heterodyne component of the correlation function can be strong (Figure 71). This heterodyning is caused by interference between the diffuse scattering and the totally reflected signal close to the specular condition i.e. where the incidence angle ai and the exit angle ae are equal. Hence, the specular reflection acts as the required static reference signal which is very intense when i < c. In future, the aim will be to control and manipulate the reference signal in order to choose the region of reciprocal space where heterodyning is desired. For diffuse scattering from a liquid surface, which becomes weaker as |i-e| is increased, such control could offer the unique possibility to quantify dynamic surface phenomena at atomic length scales.

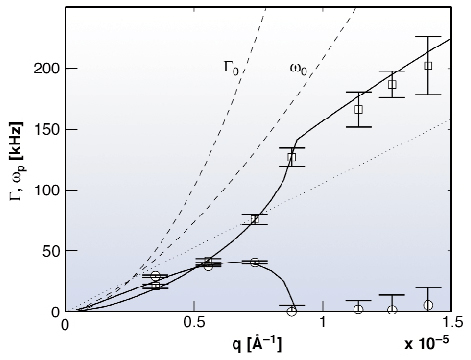
Using heterodyne grazing incidence XPCS it was recently possible to quantify the transition from propagating to over-damped capillary waves on a simple liquid surface [3]. The propagation frequency p and the damping constant of capillary waves is determined by the surface tension , the viscosity and the wave vector k. At a certain critical kc the damping gets so large that the propagating modes become unstable and eventually vanish. This influences the time-correlation function where the oscillating behaviour, which is characteristic for propagating waves, gradually disappears. Hence, by XPCS the dispersion of p and can be measured as shown in Figure 72. The data are well modelled by linear response theory (solid lines) and in particular the cross-over behaviour of p before the actual transition at q = kc is well described by the model.

 

Fig. 72: Propagation frequency p (circles) and damping constant (squares) determined by XPCS in a water/glycerol mixture at T = 12°C. The dispersion relations derived in the limit of small damping (0 q3/2, 0 q2, dashed lines) and strong damping ( q, dotted line) clearly fail to describe the observed behaviour in this transition region. Nevertheless, the data are well-modelled by linear response theory and the cross-over from propagation to over-damped behaviour is obvious at q ~ 8 x 10-6 Å-1 [3].

 

We conclude that grazing-incidence XPCS is an emerging technique with interesting perspectives for further development. In the near future, it will be applied to the study of dynamics under confinement and to investigate dynamic properties of lipid membranes and multilayers.

References
[1] I. Sikharulidze, B. Farago, I.P. Dolbnya, A. Madsen and W.H. de Jeu, Phys. Rev. Lett. 91, 165504 (2003).
[2] C. Gutt, T. Ghaderi, V. Chamard, A. Madsen, T. Seydel, M. Tolan, M. Sprung, G. Grübel, S.K. Sinha, Phys. Rev. Lett. 91, 076104; 179902(E) (2003).
[3] A. Madsen, T. Seydel, M. Sprung, C. Gutt, M. Tolan and G. Grübel, in print, Phys. Rev. Lett. (2004).

Authors
A. Madsen (a) and G. Grübel (a,b).
(a) ESRF
(b) Present address: HASYLAB (Hamburg)