Melting in two dimensions (2D) remains one of the unresolved and challenging problems in condensed matter physics. In the defect-mediated theory, the first melting step of a 2D crystal is the dissociation of dislocation pairs. This produces an anisotropic (hexatic) liquid characterised by quasi-long-range bond-orientational order while the positional order is limited to a finite correlation length. Only after a subsequent step of disclination unbinding, an isotropic phase is realised [1]. Among the systems with hexatic ordering, smectic liquid crystals are particular suitable for investigations as they can be suspended as membranes of controlled thickness over an opening in a solid frame [2].

Smectic-A (Sm-A) membranes consist of stacks of liquid layers. Upon cooling, a hexatic Sm-B phase may occur, and subsequently a 3D crystalline-B phase (Cr-B) with a hexagonal in-plane lattice and a weak coupling between the crystalline layers. We studied smectic membranes of the compound abbreviated as 4O.8, in which the Sm-A phase proceeds into Cr-B in a layer-by-layer fashion involving an intermediate hexatic Sm-B phase. With decreasing temperature the surface layers undergo transitions: from Sm-A to Sm-B at 61.1°C; from Sm-B to Cr-B at 54.5°C, well before the second set of layers start their own freezing transitions at 51.1°C. Hence, the top layer at each side of the membrane may serve as a perfect model system to study crystallisation of a liquid in 2D.

 

Fig. 86: Scattering geometry with smectic membrane and linear detector.

 

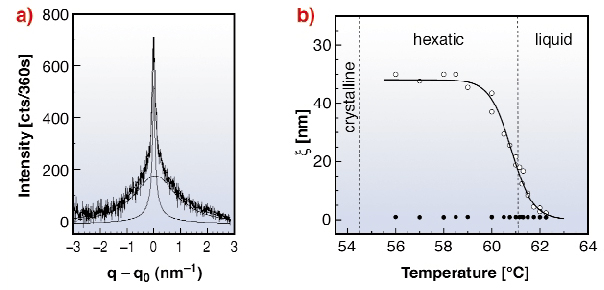
Grazing-incidence X-ray diffraction has been performed on 4O.8 membranes at beamline ID10B. The beam was focussed in the incident plane to about 24 µm and the incident and the exit angles were symmetrically set slightly above the critical angle. A linear detector was mounted parallel to the plane of the sample (Figure 86), catching in a single shot the lineshape associated with the in-plane positional ordering. Figure 87a shows for a seven-layer film the X-ray peak at q0 = 14.3 nm-1, corresponding to local in-plane hexagonal packing. It consists of a relatively narrow diffraction peak from the outermost hexatic Sm-B layers (fitted by a square-root Lorentzian) on top of a broad Lorentzian liquid peak from the five Sm-A interior layers. The integrated intensity of the former part is independent of the membrane thickness, which proves its origin in the two surface layers. The latter peak scales linearly with the number of liquid interior layers and its Lorentzian width ~ 1 nm is independent of temperature (Figure 87b). With decreasing temperature the positional correlation length of the hexatic top layers increases continuously from about 2.5 nm to more than 40 nm and then saturates. Clearly a pre-transitional growth of is present above the hexatic-isotropic transition at 61.5°C. As we did not observe any thermal hysteresis in the hexatic linewidth, this surface transition is second order. Upon further cooling of the 4O.8 membrane, another transition occurs in the top layers at 55.5°C: the hexatic peak condenses into a sharp, resolution-limited peak from the Cr-B phase. This hexatic-crystal transition is weakly first-order with an abrupt change of the in-plane positional correlations.

 

Fig. 87: (a) X-ray profile for a seven-layer membrane at 60°C with outer hexatic surface layers on a 'substrate' of five liquid inner layers. (b) Temperature dependence of the in-plane positional correlation length of the single hexatic surface layers (open circles) and the interior liquid layers (filled circles).

 

In conclusion the two-step surface freezing of a single top layer in smectic membranes as seen by grazing-incidence X-ray diffraction agrees qualitatively with defect-mediated theory. However, other measurements do not give singularities as predicted. Hence the 2D melting scenario is probably not universal and the results may depend on the specific interactions in the system.

References
[1] P.M. Chaikin and T.C. Lubensky, Principles of condensed matter physics (Cambridge University Press, Cambridge, 1995).
[2] W.H. de Jeu, B.I. Ostrovskii and A.N. Shalaginov, Rev. Mod. Phys. 75, 181 (2003).

Principal Publication and Authors
W.H. de Jeu (a), A. Fera (a), O. Konovalov (b) and B.I. Ostrovskii (a, c), Phys. Rev. E 67, 020701 (2003).
(a) FOM-Institute for Atomic and Molecular Physics, Amsterdam (The Netherlands)
(b) ESRF
(c) Institute of Crystallography, Moscow (Russia)