Thermoelectric devices convert thermal energy into electric energy and vice-versa through the Seebeck and Peltier effects, respectively. These devices are environmentally friendly and highly reliable. Because their efficiency is relatively poor when compared to conventional power plants or compressor-based refrigerators, present use is limited to critical applications, such as deep space probes and submarines. During operation, the thermoelectric material must sustain a temperature gradient and thus, its thermal conductivity must be low. In contrast, the thermoelectric material must exhibit a high electrical conductivity to minimise energy dissipation or maximise the current. Thus, a suitable thermoelectric material must behave [1] as a “phonon glass and an electron crystal”. One way to achieve the reduction in thermal conductivity of a crystal, without significant reduction of the electrical conductivity, is to insert loosely bound atoms into voids or cages of a crystalline solid.

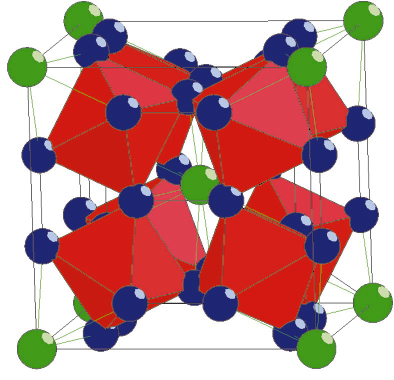
The lattice of the CoSb3 skutterudite provides voids that can be filled with rare-earth elements, R, to form filled skutterudites, RM4Sb12, where M is Co or Fe. Figure 26 shows the crystal structure of EuFe4Sb12, in which europium ions are loosely bound in their Fe-Sb cage and are believed to be responsible for the observed reduction in thermal conductivity. The experimental characterisation of the vibrational modes of the filling europium and of its cage is instrumental in understanding the role of the filling element in reducing the thermal conductivity. Among the available techniques, only nuclear inelastic scattering provides access to the partial, element specific, density of vibrational states of an atom that must have a Mössbauer active nuclide. Fortunately, all three elements in EuFe4Sb12 fulfil this condition.

Fig. 26: The crystal structure of EuFe4Sb12. The green and blue spheres are europium and antimony, respectively. The iron atoms are at the centre of the red octahedra.

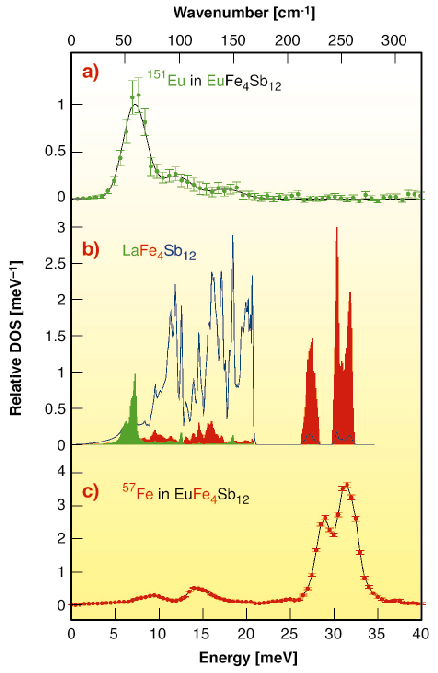
The europium-151 and iron-57 partial vibrational density of states (DOS) obtained from nuclear inelastic scattering, measured at ID22N and ID18, are shown in Figure 27, together with the calculated La, Fe, and Sb vibrational DOS in LaFe4Sb12. The iron partial DOS consists of two main peaks at ca. 29 and 33 meV and smaller contributions at 9 and 15 meV, in excellent agreement with the calculations that predict two main peaks at ca. 27.5 and 31 meV in LaFe4Sb12. The europium partial DOS was fitted with three Gaussian peaks with energies of 7.3 ± 0.1, 12.0 ± 0.4, and 17.8 ± 0.5 meV, with relative areas of 3.4 ± 0.2, 1.1 ± 0.2, and 0.5 ± 0.1, and with linewidths of 3.2 ± 0.2, 4.4 ± 0.7, and 4.4 ± 0.7 meV. These energies are in excellent agreement with the calculated energies of 7.1, 12.4, and 18.5 meV in LaFe4Sb12. The peak at 7.3 meV is characteristic of the Einstein oscillator behaviour of the europium in EuFe4Sb12. Its experimental width of 3.2 meV corresponds to a natural width of 2.7 meV, when the experimental resolution of 1.6 meV is taken into account. This small width indicates that there is at most a weak hybridisation between the europium vibrational mode at 7.3 meV and the iron vibrational mode at 9 meV. The peaks at 12.0 and 17.8 meV result from a small hybridisation of the europium vibrations with the antimony vibrations.

Fig. 27: (a) The europium partial DOS in EuFe4Sb12 obtained at 25 K by europium-151 nuclear inelastic scattering. (b) The calculated La, green, Fe, red, and Sb, blue, vibrational DOS in LaFe4Sb12. (c) The iron partial DOS in EuFe4Sb12 obtained at 295 K by iron-57 nuclear inelastic scattering.

In conclusion, the europium-151 and iron-57 nuclear inelastic scattering experiments on EuFe4Sb12 reveal the localised nature of the europium vibrations at 7.3 meV, the strong decoupling of the iron and europium vibrations, and the weak coupling of the europium and antimony vibrational modes. Hence, nuclear inelastic scattering has proven to be a powerful technique for the investigation of the lattice dynamics of the filled skutterudites, compounds in which this lattice dynamics strongly influences their thermoelectric properties. Antimony-121 nuclear inelastic scattering experiments will soon be undertaken at ESRF and are expected to complete the picture of the lattice dynamics in EuFe4Sb12. To date, the filled skutterudites probably provide the best example of an Einstein oscillator [2]. However, the precise mechanism by which the addition of this filling atom, that essentially behaves as a harmonic oscillator, yields a significant reduction in the thermal conductivity of the filled skutterudites is still to be understood.

 

References

[1] G. A. Slack, “New materials and performance limits for thermoelectric cooling,” CRC Handbook of Thermoelectrics, ed. D. M. Rowe (CRC Press, Boca Raton, FL, 1995), pp. 407.
[2] A. Einstein, Ann. Phys. 22, 180 (1907).

Principal Publication and Authors

G.J. Long (a), R.P. Hermann (b), F. Grandjean (b), E.E. Alp (c), W. Sturhahn (c), C. E. Johnson (c), D.E. Brown, (c), O. Leupold (d), and R. Rüffer (d), Phys. Rev. B 71, 140302 (2005).
(a) Department of Chemistry, University of Missouri-Rolla (USA)
(b) Department of Physics, University of Liège, Sart-Tilman (Belgium)
(c) Advanced Photon Source, Argonne National Laboratory, Illinois (USA)
(d) ESRF