Atomic diffusion in amorphous and nanocrystalline alloys has been a subject of great interest, as it governs the structural relaxation and associated changes in the physical properties in these alloys. Depth profiling techniques like radioactive tracer and secondary ion mass spectrometry are most widely used for such studies, however, these techniques are limited by their depth resolution which is of the order of a few tens of nanometres. This is a severe limitation in the study of metastable systems like amorphous and nanocrystalline phases, where diffusion lengths of more than a few nanometres may be difficult to achieve, as annealing temperatures have to be kept low in order to avoid structural changes. Dynamic techniques like Mössbauer spectroscopy or nuclear forward scattering on the other hand are limited by the time window over which they are sensitive to atomic diffusion. For example, diffusivities accessible using 57Fe Mössbauer spectroscopy lie in the range 10-12 to 10-13 m2/s.

In the present work we demonstrate the possibility of using nuclear resonance scattering from isotopic multilayers for studying self-diffusion of Mössbauer isotopes over a wide range of diffusivity. For a reasonable range of annealing times, a diffusivity range of 10-26 m2s-1 to 10-18 m2s-1 could be made accessible. At the same time, this technique is sensitive enough to measure diffusion lengths as small as 0.1 nm, which is more than an order of magnitude larger than the sensitivity of conventional depth profiling techniques. The systems selected for present studies are amorphous and nanocrystalline alloys of iron.

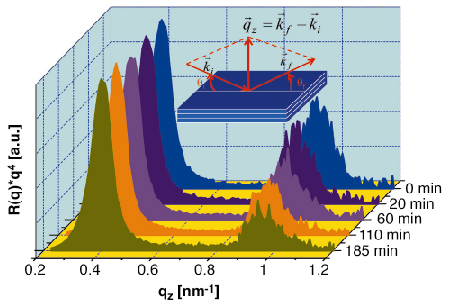
Figure 6 shows nuclear resonance reflectivity of isotopic multilayer of nanocrystalline FeNZr having structure [57FeNZr (4nm)/FeNZr (3nm)]20. The film is chemically homogeneous, however, scattering contrast between adjacent layers emanates due to the nuclear resonance scattering of 14.413 keV X-rays from 57Fe isotope. Measurements were done at beamline ID22N.

Fig. 6: Nuclear resonance reflectivity of the [57FeNZr (4nm)/FeNZr (3nm)]20 multilayer taken at the Mössbauer resonance energy of 57Fe (14.413 keV), as a function of annealing time at 393 K.

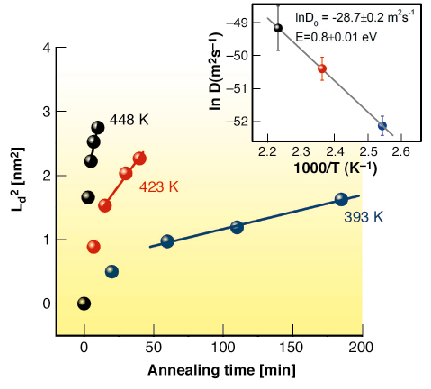
A Bragg peak around qz = 0.9 nm-1 is observed due to isotopic periodicity. As the multilayer is annealed, iron atoms diffuse across the isotopic interfaces, and the intensity of the Bragg peak decays with annealing time, yielding the diffusion length through the relation, ln[I(t)/I(0)] = -42n2Ld2/d2, where I(t) is the intensity of the Bragg peak after annealing time t, n is the order of Bragg reflection, Ld is the diffusion length and d is the bilayer periodicity. Figure 7 gives Ld as a function of annealing time at three different temperatures. It increases initially at a faster rate and after a certain annealing time the rate becomes constant. The initial faster increase in the diffusion length is associated with the structural relaxation in the system, similar to amorphous alloys. This relaxation is associated with the relaxation of the highly disordered grain boundary region, stress relaxation in the film and annealing out of the defects inside the nanocrystals. After sufficiently long annealing time, the diffusion length increases linearly with annealing time and the diffusivity was obtained by a linear fit using the relation: Ld2 = 2D(T)t.

Fig. 7: Evolution of interdiffusion length Ld as a function of annealing time at different temperatures. The inset shows the Arrhenius behaviour of diffusion coefficient with isothermal annealing temperature, yielding the activation energy and pre-exponent factor for self-diffusion of Fe.

The diffusivity follows Arrhenius type behaviour with temperature, as shown in the inset of Figure 7. The solid line in the figure is a fit to the experimental data obtained using the relation D = D0exp(-E/kBT), where E is the activation energy and D0 is the pre-exponential factor which contains the details of the diffusion mechanism. The obtained values of activation energy and pre-exponential factor are E = 0.8 ± 0.01 eV and D0 = exp (–28.67 ± 0.23). The activation energy for self-diffusion of Fe in the present system is significantly lower than that in the amorphous FeN of similar composition [1]. This result is in general agreement with the earlier studies where the low activation energy for diffusion in nanocrystalline alloys has been attributed to a higher density of grain boundaries. Further, the observed values of D0 and E suggest that the mechanism of diffusion in this system is similar to that in amorphous alloys [2].

It may be noted that the high sensitivity of the present technique enables one to clearly see the initial variation in the diffusivity because of the structural relaxation in the system even at temperatures as low as 393 K, although the typical diffusion lengths involved are of the order of 0.1 nm.

 

References

[1] M. Gupta, A. Gupta, S. Rajagopalan, and A. K. Tyagi, Phys. Rev. B 65, 214204 (2002).
[2] F. Faupel, W. Frank, M.P. Macht, H. Mehrer, K. Rätzke, H.R. Schober, S.K. Sharma, H. Teichler, Rev. Mod. Phys. 75, 237 (2003).

Principal Publication and Authors

A. Gupta (a), M. Gupta (a,b), S. Chakravarty (a), R. Rüffer (c), H-C Wille (c), O. Leupold (c), Phys. Rev. B 72, 014207 (2005).
(a) UGC-DAE Consortium for Scientific Research, Indore (India)
(b) Laboratory for Neutron Scattering, ETH Zürich & PSI, Villigen (Switzerland)
(c) ESRF