- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2005
- High Resolution and Resonance Scattering
- Improving X-ray Crystal Spectrometers with Position-sensitive Detectors
Improving X-ray Crystal Spectrometers with Position-sensitive Detectors
Inelastic X-ray scattering (IXS) spectrometers are often based on analyser crystals operating in the Rowland circle geometry. The crystal is used to select a desired bandwidth of radiation scattered by the sample and simultaneously to focus the gathered radiation onto an X-ray detector. To achieve the focusing properties, the crystal wafers are typically bent to have a spherical or cylindrical shape. Bending, however, increases the bandpass of the crystal due to elastic deformations. This is desirable in many applications where high flux is preferred over a high energy-resolving power. In cases where the resolving power is needed to exceed 105, these elastic deformations may become too large and other solutions need to be sought. For instance, in many very high energy resolution applications so-called diced analyser crystals are utilised. In this scheme, thousands of small flat crystals (dices or cubes) are arranged to mimic the shape of the spherical surface. Since each crystalline is flat, it behaves as a perfect single crystal with a very narrow reflection width. However, the price to pay is that the finite size of the cubes causes a geometrical contribution to the resolution function, of the form ![]() E/E = c/R cot
E/E = c/R cot![]() , where c is the dice size (typically c = 0.7 mm), R the crystal curvature radius, and
, where c is the dice size (typically c = 0.7 mm), R the crystal curvature radius, and ![]() the Bragg angle.
the Bragg angle.
 |
|
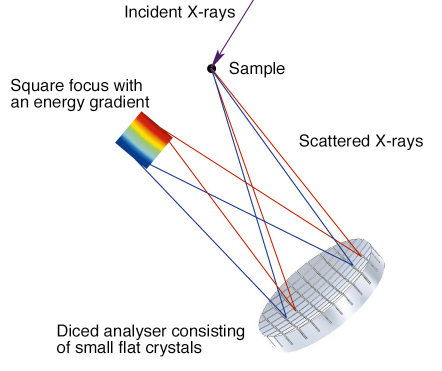
Fig. 14: A diced analyser crystal acts like a prism, i.e. it sorts out the spectrum of scattered radiation in space. This enables an analysis of the photon energy by observing its position in the focus. |
So far, this cube-size contribution was considered inevitable. The only ways to minimise this effect have been reducing the cube size c, increasing the bending radius R, and selecting a photon energy and the reflection as close to backscattering as possible. These constraints have for instance forced the construction of very large experimental stations (e.g. at ESRF ID16 R = 6.5 m and ![]() = 89.98°). In a recent study at ID16 it was found that the cube-size contribution can be eliminated by noting that it corresponds to a dispersion of photon energies within the spatial focus. The focus of the analyser was found to be a square with dimensions 2c x 2c, with a position-energy relationship such that constant-Bragg-angle contours were observed. When c/R << sin(2
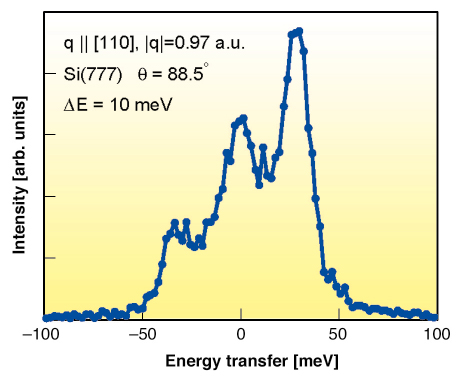
= 89.98°). In a recent study at ID16 it was found that the cube-size contribution can be eliminated by noting that it corresponds to a dispersion of photon energies within the spatial focus. The focus of the analyser was found to be a square with dimensions 2c x 2c, with a position-energy relationship such that constant-Bragg-angle contours were observed. When c/R << sin(2![]() ), only a small part of the ring-like contour is observed and the position-energy dependence is close to linear (see Figure 14). The detector used in this experiment was a CMOS-based Medipix2 photon-counting pixel detector with a pixel size of 55 µm and sensitive area of 14 x 14 mm2 [1]. Using this setup with R = 1 m, an unprecedented spectrometer resolution of 23 meV was achieved at 9.9 keV, and 10 meV at 13.8 keV, utilising the Si(555) and Si(777) reflections, respectively (see an example of a phonon spectrum in Figure 15). Without this method the resolution would have been 190 meV and 250 meV, respectively. This can be compared to the resolution at 7 meV achieved typically with a 6.5-m Rowland circle spectrometer at a photon energy of 13.8 keV.
), only a small part of the ring-like contour is observed and the position-energy dependence is close to linear (see Figure 14). The detector used in this experiment was a CMOS-based Medipix2 photon-counting pixel detector with a pixel size of 55 µm and sensitive area of 14 x 14 mm2 [1]. Using this setup with R = 1 m, an unprecedented spectrometer resolution of 23 meV was achieved at 9.9 keV, and 10 meV at 13.8 keV, utilising the Si(555) and Si(777) reflections, respectively (see an example of a phonon spectrum in Figure 15). Without this method the resolution would have been 190 meV and 250 meV, respectively. This can be compared to the resolution at 7 meV achieved typically with a 6.5-m Rowland circle spectrometer at a photon energy of 13.8 keV.
 |
|
Fig. 15: Phonons in aluminium measured with 10 meV resolution with a IXS spectrometer based on 1-m Rowland circle and a position sensitive detector. |
It was thus demonstrated that new photon-counting position-sensitive detectors can be used to enhance the resolution of IXS spectrometers considerably. The presented method allows for a marked increase in resolving power, while preserving all counted photons so that the improvement in resolution is not accompanied by any loss of signal intensity. This gives new possibilities for the construction of a much more powerful and compact high-resolution IXS instruments than has been possible this far, which may affect the design of future non-resonant and resonant IXS spectrometers.
References
[1] X. Llopart, M. Campbell, R. Dinapoli, D. San Segundo, E. Pernigotti, IEEE Trans. Nucl. Sci. 49, 2279-2283 (2002).
Principal Publication and Authors
S. Huotari, Gy. Vankó, F. Albergamo, C. Ponchut, H. Graafsma, C. Henriquet, R. Verbeni and G. Monaco, J. Synchrotron Rad. 12, 467-472 (2005).
ESRF



