Colloidal systems are ubiquitous in everyday life involved in many consumer and industrial products such as milk, cosmetics and paint. They also allow us to simulate many atomic-scale phenomena on a larger dimension. Model systems such as hard-sphere and sticky hard-sphere colloids have been extensively investigated over the past several decades. In recent years, short-ranged attractive colloids have received renewed interest in terms of their dynamical properties [1]. Mode coupling theory and computer simulations have predicted two different glass transitions in these systems. In hard-sphere like repulsive colloids, the glassy state is an alternative to crystalline order at high volume fractions. The ergodicity in the repulsive glass is lost due to blocking of particle diffusion by the dense surrounding cages formed by their nearest neighbours [1]. With the introduction of a short-ranged attraction of magnitude a few kBT (where kB is the Boltzmann constant) and range a few percent of the size of the particle, a different type of glassy state emerges that is called an attractive glass, where the particle motion is jammed by the strong stickiness. Attractive glass is a unifying term to describe the wide variety of dynamical arrest such as gelation, glassification, non-ergodicity transition, etc., induced by the stickiness.

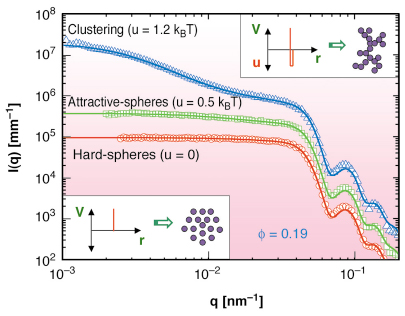
Ultra small-angle X-ray scattering (USAXS) is a versatile technique for probing the subtle to dramatic changes in structure at different length scales in short-ranged interacting colloids [2]. A convenient model suspension for investigating the different facets of these systems is sterically stabilised silica colloids suspended in certain alkanes (e.g. n-dodecanol). In this case, a thermally reversible transition between repulsive and attractive colloids can be induced by lowering the temperature. Experiments were performed at beamline ID02. Figure 40 shows the typical evolution of the scattered intensity [I(q)] as a function of the scattering wave vector (q) at an intermediate volume fraction of 0.19. I(q) can be decomposed into the structure factor of interparticle interactions [S(q)] and the single particle scattering function which is dominant at high q values. S(q) can be modelled in terms of an interparticle potential [V(r)] involving a repulsive hard-sphere part, and an attractive square-well with depth, u, and width a few percent of the diameter of the particles within the Percus-Yevick approximation [2]. As the particles become attractive, they stick together to form clusters which is indicated by the excess scattering at small q ranges and in this case S(q) involves both the interparticle interaction and the morphology of these clusters. The quantitative scale and the wide q range provided by USAXS allow decomposition of the different contributions to I (q) and an accurate deduction of the parameters of interparticle potential.

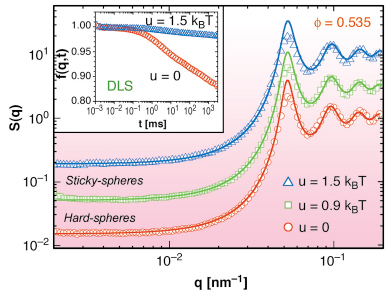
Figure 41 presents the subtle variation of S(q) when the system transforms from hard-sphere repulsive to short-ranged attractive colloids at high volume fraction ( ~ 0.535). With the onset of attraction, particles stick together but there is no signature of clustering. The inset shows the corresponding changes in the intermediate scattering function [f(q,t)] derived from dynamic light scattering (DLS) performed on the same sample. In the repulsive state (u = 0), f(q,t) shows typical features of a repulsive colloidal glass. While in the attractive case (u ~ 1.5 kBT), f(q,t) remains close to 1 indicating that the particle dynamics are nearly frozen (jammed). This demonstrates a transition from repulsive to attractive glass as the depth of the attractive potential is systematically increased. Furthermore, the static S(q) shows only subtle changes while the dynamics and rheological properties vary dramatically [2] thereby establishing the kinetic nature of these glass transitions.

A combination of USAXS, DLS and bulk rheology provided complimentary information which allowed us to identify different dynamical transitions in short-ranged attractive colloids [2]. Observed features are broadly in agreement with recent theoretical predictions and computer simulations [1].

Fig. 40: Evolution of the microstructure of a colloidal system as a function of the strength of short-ranged attraction. Solid lines represent model for the corresponding interactions. The lower and the upper insets depict repulsive hard-sphere like suspension and clustering of particles when the depth of the attractive potential exceeds kBT. For clarity the green and blue curves are displaced by a factor 3 and 10, respectively.

 

Fig. 41: Subtle changes in the static structure factor with the depth of attractive potential (u) at high volume fraction (~ 0.535). The solid lines represent models for S(q). The inset shows a more dramatic variation of the intermediate scattering function obtained from dynamic light scattering. For clarity the green and blue curves are displaced by a factor 3 and 10, respectively.

 

References

[1] F. Sciortino and P. Tartaglia, Adv. Phys., 54, 471 (2005), and references therein.
[2] T. Narayanan, M. Sztucki, G. Belina, and F. Pignon, Phys. Rev. Lett., 96, 258301 (2006).

Principal Publication and Authors

M. Sztucki (a), T. Narayanan (a), G. Belina (a), A. Moussaïd (a), F. Pignon (b) and H. Hoekstra (c), Phys. Rev. E, 74, 051504 (2006).
(a) ESRF
(b) Laboratoire de Rhéologie, CNRS, Grenoble (France)
(c) Katholieke Universiteit, Leuven (Belgium)