Langmuir films of long chain amphiphiles at the air-water interface present different phases depending on temperature and surface pressure (the difference between the surface tension of pure water and the actual surface tension in presence of the film = H20– ). Their phase transitions were first identified by isotherm measurements (surface pressure as a function of molecular area for a fixed temperature). The first grazing-incidence X-ray diffraction (GIXD) experiments carried out directly on monolayers at the air-water interface were reported in 1987 [1]. GIXD has now become the primary technique used to determine the structure of amphiphilic monolayers on water, allowing the determination of unit cell parameters, molecular tilt angle and azimuth of tilt direction. It is however generally considered that going beyond this simple unit cell characterisation is impossible.

We have recently developed a different method, consisting of a careful extraction of the structure factors from the diffraction data followed by fitting of molecular parameters, which allowed us to obtain sub-molecular information [2]. The structure factor calculations are performed using the SHELX-97 program developed by George Scheldrick. We use the known chemical structure of fatty acid molecules by imposing atomic coordinate in a molecular model which allows us to fit relevant parameters such as hydrocarbon backbone plane azimuth, head-group rotation, or gauche defects in the hydrocarbon chain. Sterically impossible configurations are automatically rejected by SHELX.

Molecular parameters have a marked influence on the calculated structure factors and can be determined by model fitting. For example, the intensity ratio between reflections is very sensitive to the orientation of the backbone planes whereas the Bragg rod profiles along the vertical are sensitive to the conformation defects. Untilted phases of fatty acids have been investigated using a systematic exploration of all relevant parameters [2]. We were able to determine the orientation of the chain backbone planes and of the carboxylic head-groups directly, measurements that were previously inferred from 3d measurements. Our method allowed us to evidence a new phase of symmetry p2gm at high pressure, corresponding to a minimum in lattice energy, which had never been observed before.

The use of a simulated annealing technique allows a large reduction in computation time which enables the determination of conformational defects. Simulated annealing is a Monte-Carlo method where the “temperature” is progressively decreased in order to avoid local 2 minima. With a proper temperature decrease scheme, the results obtained using the simulated annealing algorithm do not differ from those obtained by systematic variation of all parameters. The statistics of conformation defects were estimated by considering large super-cells composed of at least 18 unit cells.

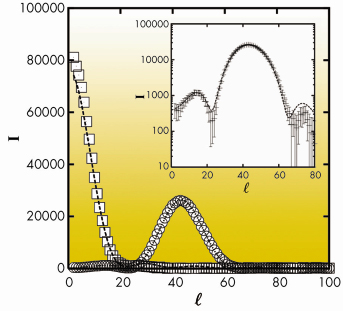
Fig. 55: Experimental Bragg rods corresponding to the (02) (squares) and (11) (circles) reflections for behenic acid in the L2” phase of behenic acid at 0.2 mN/m and T = –2.5°C. The dashed lines represent best fits. The same curves are shown in log scale in the insert in order to emphasise low intensity details.


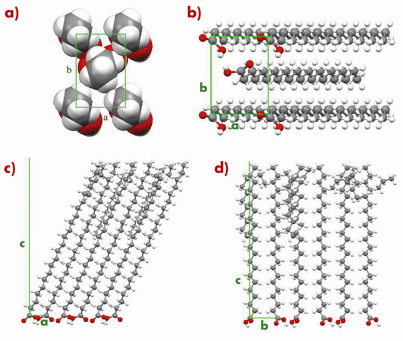
An example is given in Figures 55 and 56 for the so-called L2” phase of behenic acid (the fatty acid with a 21 carbon chain) at 0.2 mN/m and T=–2.5°C. Figure 55 shows that an excellent agreement is obtained for the Bragg rod profiles. In Figure 56, the most interesting features are the co-planarity of chains and head-groups, an angle of 45° between the backbone planes, and, though the L2” is a crystalline phase, the presence of many defects at the chain ends.

The method we have used is quite general, it uses data in the PDB format, and could be applied, for example to 2-dimensional peptide or protein crystals.

Fig. 56: L2” phase of behenic acid at 0.2 mN/m and T = -2.5°C. (a) Transverse cell seen from the methyl groups. (b) Bottom view of the unit cell showing the headgroup organisation. Projection of the super-cell with 18 molecules in the (a, c) (c) and (b, c) (d) planes.

 

References

[1] K. Kjaer, J. Als-Nielsen, C.A. Helm, L.A. Laxhuber, H. Möhwald, Phys. Rev. Lett. 58, 2224-2228 (1987); P. Dutta, J.B. Peng, B. Lin, J.B. Ketterson, M. Prakash, P. Georgopoulos, S. Ehrlich, Phys. Rev. Lett. 58, 2228-2231 (1987); S. Grayer Wolf, L. Leiserowitz, M. Lahav, M. Deutsch, K. Kjaer, J. Als-Nielsen, Nature 328 63-66 (1987).
[2] J. Pignat, J. Daillant, L. Leiserowitz, F. Perrot, J. Phys. Chem. B 110, 22178-22184 (2006).

Principal publication and authors

J. Pignat (a,b), J. Daillant (a), S. Cantin (b), F. Perrot (b), O. Konovalov (c), Thin Solid Films 515, 5691-5695 (2007).
(a) LIONS/Service de Chimie Moléculaire, CEA-Saclay, Gif-sur-Yvette (France)
(b) LPPI, université de Cergy-Pontoise (France)
(c) ESRF