It is an intriguing fact that in many complex materials superconductivity – a state of matter where charge can move through a lattice without any resistance – often exists in close proximity to what appears to be exactly the opposite: the static spatial ordering of charge. But despite intense research efforts, the question if or under which circumstances electronic order competes, coexists with or supports superconductivity remains mostly controversial.

A particularly interesting example is the charge density wave (CDW) system 1T-TaS2. For this material, measurements of the electrical resistivity revealed that external pressure stabilises a superconducting phase, which again exists in very close proximity to electronically ordered phases. Whether and how this superconductivity is related with the CDW on a microscopic level remained, however, unknown from the experimental point of view.

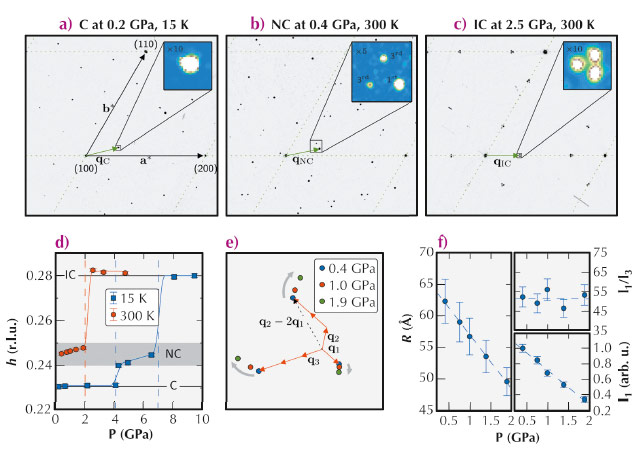
To clarify this issue, we performed pressure dependent X-ray diffraction (XRD) experiments at beamline ID09A. These state-of-the-art synchrotron experiments provide direct access to the microscopic properties of electronically ordered phases. More specifically, the periodic lattice modulations associated with the CDW lead to so-called superlattice reflections, which enable a determination of the amplitude and the modulation wave vector (q-vector) of the CDW. Representative XRD data obtained during this experiment are shown in Figure 39.

At low pressure and low temperature 1T-TaS2 exhibits a commensurate CDW (C-CDW), which is often described as a Mott-insulating phase and which displays a commensurate modulation wave vector qC as shown in Figure 39a. Upon applying external pressure, this phase is rapidly suppressed and a so-called nearly commensurate CDW (NC-CDW) appears. The NC-CDW is characterised by a domain-like structure, consisting of commensurate C-CDW domains separated by metallic domain walls, called discommensurations. The latter can be understood as defects in the electronic C-CDW lattice. But unlike ordinary defects, these discommensurations themselves form a self-organised, long-range ordered structure [2] that causes the sharp spots in Figure 39b. The corresponding modulation wave vector is labelled as qNC and its incommensurability Δ=|qNC-qC| is determined by the distance R between neighbouring commensurate domains (cf. Figure 40 and Figure 39e): R ~ 1/Δ [3]. The other reflections shown in the inset of Figure 39b and Figure 39e are of higher order and their intensities are related to the spatial structure of the discommensurations.

Diffraction patterns in the commensurate (C), nearly commensurate (NC) and incommensurate (IC) phase

Fig. 39: (a), (b) and (c): Diffraction patterns in the commensurate (C), nearly commensurate (NC) and incommensurate (IC) phase, respectively. (d) In-plane component q as a function of pressure at two temperatures. qNC exhibits a clear pressure dependence. (e) Pressure evolution of the nearly commensurate super lattice reflections (the same region as in the inset of (b) is shown). q1=qNC-qC , q2 and q3 are obtained by 120° rotations. (f) Pressure dependence of R and the intensities of the first (I1) and third (I3) order superlattice peak.

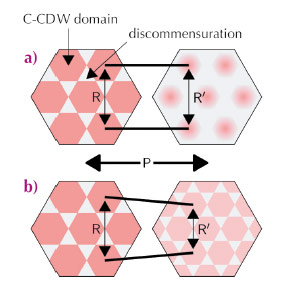
Up to now it was proposed that the insulating C-CDW domains melt with increasing pressure and, hence, the metallic inter-domain regions broaden and become interconnected as sketched in Figure 40a. Such a scenario would have distinct consequences for the observed superlattice reflections: (i) R remains essentially constant with increasing pressure and therefore ∆ will not change significantly; (ii) The broadening of the domain walls would result in a substantial change of the intensity ratio between the first and higher order satellite reflections.

Real space pressure evolution of the NC phase

Fig. 40: Real space pressure evolution of the NC phase (a) according to Sipos et al. [1] and (b) concluded from X-ray diffraction.

However, these two characteristic changes of the XRD patterns are not observed experimentally, as demonstrated in Figure 39f. Instead we found that the difference vector q1 substantially changes upon increasing pressure (Figure 39e) implying that R decreases pronouncedly. At the same time the intensity ratio between first and higher order reflections remains constant, which indicates that the domain boundaries do not broaden significantly with increasing pressure. We found that this situation does not change upon cooling below the superconducting transition temperature.

These observations therefore provide strong experimental evidence for the scenario indicated in Figure 40b, where the lattice of discommensurations shrinks without forming large interconnected metallic regions. Such a behaviour leads to the astonishing conclusion that the ordered structure in total becomes superconducting. In other words, not only the metallic regions support superconductivity, but the whole electronic crystal illustrated in Figure 40b forms a coherent macroscopic superconducting state.

Principal publication and authors

T. Ritschel (a,b), J. Trinckauf (a), G. Garbarino (c), M. Hanfland (c), M.V. Zimmermann (d), H. Berger (e), B. Büchner (a,b), and J. Geck (a), Physical Review B 87, 125135 (2013).

(a) Leibniz Institute for Solid State and Materials Research IFW Dresden (Germany)

(b) Institute for Solid State Physics, Dresden Technical University (Germany)

(c) ESRF

(d) Hamburger Synchrotronstrahlungslabor (HASYLAB) at Deutsches Elektronensynchrotron (DESY), Hamburg (Germany)

(e) Ecole Polytechnique Federale de Lausanne (Switzerland)

References

[1] Sipos et al., Nature Materials 7, 960 (2008).

[2] Spijkerman et al., Physical Review B 56, 13757 (1997).

[3] Nakanishi et al., Journal of the Physical Society of Japan 43, 1509 (1977).