Phonons are quasiparticles of lattice vibrations with certain energy and momentum. In physics textbooks, they are introduced for a periodic structure of atoms connected by harmonic springs. The eigenmodes of the vibrations in harmonic crystals are those lattice motions that are uncoupled. Any quantum of energy in such phonon modes would remain in this mode forever and makes the entire crystal oscillate at the corresponding eigenfrequency. To explain the phenomena of a finite heat transport of dielectric materials and the thermal expansion of crystals, the springs have to be anharmonic. This leads to the coupling of modes and therefore the respective phonons can be interconverted if the respective quasiparticle properties of energy and momentum are conserved.

For future materials and devices it would be of high interest to understand and manipulate the coupling of phonons with frequencies in the GHz to THz range in complex materials. This is important for nanoscale heat transport, thermoelectric materials and phonon computing.

In this work we present a scheme to excite high-amplitude, nanometric and narrowband phonon wave packets with a certain energy and momentum. The use of time-resolved X-ray diffraction at beamline ID09B enabled us to measure the occupation of the phonon modes composing these wave packets transiently. As the phonon coupling changes the occupation of the modes, the coupling between specific phonon modes can be measured.

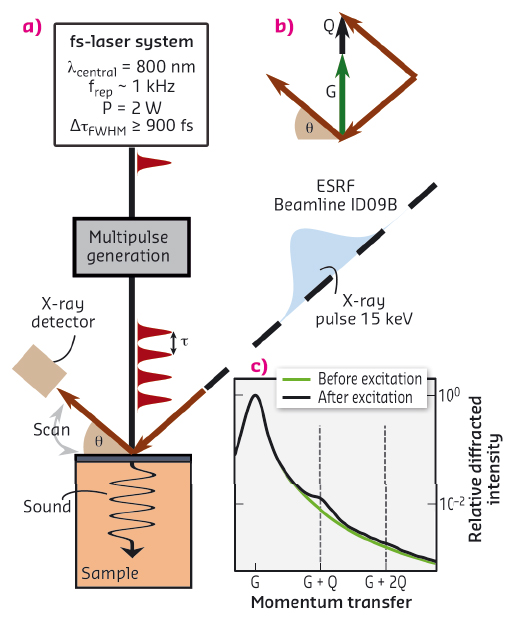
As a first example of “nonlinear phononics”, we present the second harmonic generation of phonons with a wavelength in the nanometre range. This is analogous to nonlinear optics where photons interact with each other in a nonlinear crystal. We excited a narrowband phonon wave packet by shining a train of four ultrashort laser pulses with a temporal displacement t on an epitaxially-grown nanometric SrRuO3 metal film on top of a SrTiO3 substrate, as shown in Figure 89a. The metal film’s temperature rose rapidly due to the absorption of the laser pulses. The quasi-instantaneous occupation of phonons leads to an expansive force on the crystal via the anharmonicities. This expansion triggers a hyper-sound wave entering the substrate [1]. Using four pulses, the metal film should oscillate with the frequency 1/τ and generate a phonon wave packet with this frequency propagating through the substrate.

Experimental setup to excite narrowband phonon wave packets and detect them transiently with synchrotron X-ray pulses

Fig. 89: (a) Experimental setup to excite narrowband phonon wave packets and detect them transiently with synchrotron X-ray pulses. (b) Wave vector diagram of a phonon scattering process, where G is a reciprocal lattice vector and Q the phonon wave vector. (c) Measured rocking curves with and without excitation.

We used X-ray diffraction to observe the transient spectral content of the excited phonon wave packet. X-rays scatter from crystal lattice planes described by their corresponding reciprocal lattice vector G and phonons given by their wave vector Q, as depicted in Figure 89b [2]. Here, an incident X-ray pulse was diffracted by the lattice planes of the SrTiO3 substrate resulting in the peak at G in Figure 89c before and after excitation with the laser pulses. After excitation, additional diffraction at G+Q was detected, which is evidence that a narrowband phonon wave packet with wave vector Q was excited.

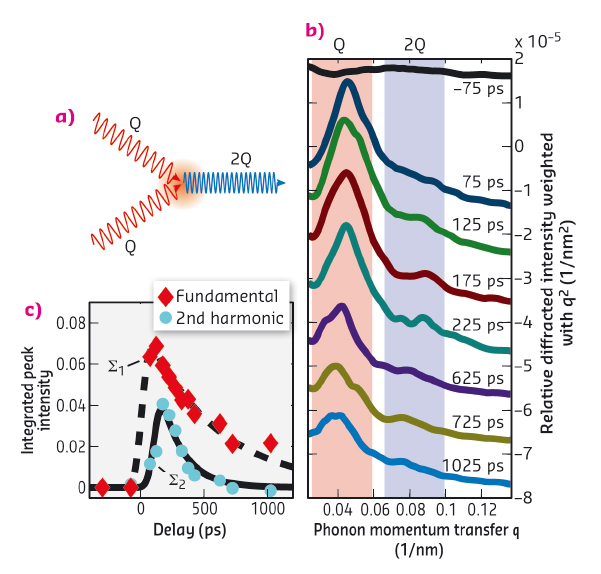
Second harmonic generation of monochromatic phonon wave packets

Fig. 90: Second harmonic generation of monochromatic phonon wave packets. (a) The scattering process of two phonons with wavevector Q generate a phonon with the doubled wavevector 2Q. (b) Scattering intensity weighted with q2 of the excited fundamental (red) and its second harmonic (blue). (c) The transient change in the integrated scattering intensity of the fundamental and its second harmonic.

To demonstrate second harmonic generation of monochromatic phonon wave packets, as depicted in Figure 90a, we repeated the time-resolved X-ray diffraction experiment with a slightly thicker metal film that absorbs more optical energy and used only two laser pulses while keeping the total incident laser energy constant. This doubles the local atomic displacement and quadruples the acoustic energy density of the wave packet. This increased the up-conversion efficiency of phonons at the expense of monochromaticity according to the higher wave packet localisation in space. Figure 90b shows the diffracted intensity weighted with q2 for better visibility of peaks at high q. The red shaded region is the diffraction related to the excited wave vector Q and the blue region highlights diffraction assigned to the second harmonic with the wave vector 2Q. It can be seen that the second harmonic 2Q starts rising 125 ps after excitation of Q. This delay is evidence that the second harmonic is not directly excited by the laser pulses, rather it is generated by anharmonic coupling within the phonon wave packet. Figure 90c shows the transient change of the integrated intensity of the peaks corresponding to the wave vectors Q (∑1) and 2Q (∑2). In addition to the delay between both maxima, one can easily see that the second harmonic damps out more rapidly than the phonons with wave vector Q, which is in accordance with known phonon damping theory.

 

Principal publication and authors

Second harmonic generation of nanoscale phonon wave packets, A. Bojahr (a), M. Gohlke (a),  W. Leitenberger (a), J. Pudell (a), M. Reinhardt (b), A. von Reppert (a), M. Roessle (a), M. Sander (a),  P. Gaal (b) and M. Bargheer (a,b) PRL 115, 195502 (2015); doi: 10.1103/PhysRevLett.115.195502.
(a) Institut für Physik und Astronomie, Universität Potsdam (Germany)
(b) Helmholtz Zentrum Berlin (Germany)

 

References

[1] D. Schick et al., Struct. Dyn. 1, 064501 (2014).
[2] A. Bojahr et al., Opt. Express 21, 21188 (2013).