Does nuclear resonant scattering violate reciprocity?

The original text by Rayleigh reads "If in a space filled with air, which is partly bounded by finitely extended fixed bodies and is partly unbounded, sound waves be excited at any point A, the resulting velocity potential at a second point B is the same both in magnitude and phase, as it would have been at A, had B been the source of sound". 

A large class of physical processes can be described by wave scattering theory; indeed, more generally, one can speak about the scattering of elastic and sound waves (classical mechanics), of electromagnetic waves (electrodynamics) or of particles (quantum mechanics). As long since documented in the literature, and also suggested by one’s own physical intuition, the observed signal should not change when reversing the position of source and detector in a general wave scattering experiment. This expectation, called the reciprocity principle, was therefore generalised for more complex scattering systems and is indeed fulfilled in most cases.

One of the earliest applications of the reciprocity principle has appeared in the field of antenna theory in radio communication. Why is it possible to use the same antenna for creating and receiving radio signals? The theoretical answer based on reciprocity seems to be very simple and was given at the beginning of the twentieth century. Nonreciprocal devices like circulators (transmitters) and isolators (blocking destabilising reflections arriving back into sources) are routinely used in microwave optics, but similar devices are in high need for applications in optical fibre systems.

The reciprocity principle was based originally on intuitive analogy, but it did not follow directly from first principles, and, therefore, it is not necessarily fulfilled. Reciprocity is a theorem, which can be proven only for certain scattering problems with certain limits of validity. The reciprocity related publications span the whole twentieth century, as summarised in the review paper of Potton [1].

What is reciprocity? In many works, it is simply related to time reversal symmetry because the transposition of 'action' (source) and 'reaction' (detector) is similar to the effect of reversal of the direction of the waves, in other words, reversal of the time. The optical reciprocity theorem, however, revealed that absorption, which violates time reversal invariance, maintains reciprocity in polarisation independent cases. In parallel, according to the original reciprocity principle, namely, invariance under the interchange of source and detector, one could have the impression that reciprocity is identical to a rotation by 180°. However, this latter interpretation also proves false since there exist scatterers with no 180° rotational symmetry but fulfilling the reciprocity principle. Reciprocity is more general than time reversal invariance, and it also differs from rotational invariance, as it is explained in the general reciprocity theorem that has been formulated recently [2].

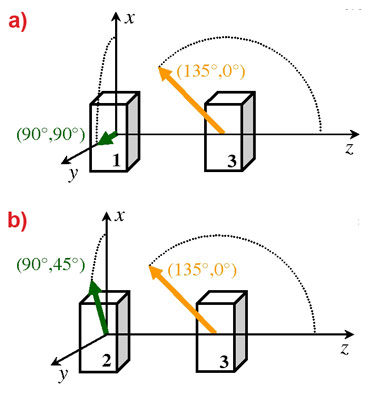
In our experiment, reciprocity and its violation was studied. Our aim was twofold: to demonstrate that reciprocity violation can be a remarkably strong effect, and to check easily whether reciprocity violation is present or missing. Nuclear forward scattering (NFS) of synchrotron radiation was applied in two experimental arrangements of ferromagnetic scatterers (S1, S2) (Figure 1). Both scatterers consist of two 6 μm thick ⁵⁷Fe foils (L_i, i=1,2,3) uniformly magnetised in a field of 0.19 T by means of permanent magnets. The foils L₁, L₂ and L₃ are respectively magnetised in directions given by the polar angles (90°, 0°), (90°, 45°) and (135°, 0°), where the coordinate system is chosen with the z axis being parallel to the beam and the y axis being parallel to the direction of the sigma-polarisation. The first scatterer S1 was a combination of an L₁ foil and of an L₃ foil, while the second scatterer S2 was formed by an L₂ foil and an L₃ foil. For each scatterer, the scattering spectrum was compared to that of the reciprocal scattering. The interchange of source and detector position was realised by a 180° rotation of the whole sample holder around the x axis of the coordinate system [2]. The four time spectra (count vs. time diagrams) shown in Figure 2 were measured at the nuclear resonance end station ID22N using an Si(840) channel cut sigma-analyser.

Figure 1. Geometrical arrangement for a) the (magnitude) reciprocal and b) the nonreciprocal case, respectively. The synchrotron beam propagates in the direction of the z axis and gets scattered on foils L1 (1), L3 (3) (reciprocal scattering) or L2 (2), L3 (3) (nonreciprocal scattering). The thick arrows show the direction of the magnetic field in the iron foils, also given by the polar angles.

The experimental results and the corresponding computer simulations made by our computer program [3] are shown in Figure 2. The slight imperfection in the agreement between measurement and simulation is due to, and provides information about, non-perfect uniformness in the foil thickness and the magnetic field inside. The experiment kept these undesired influences under control by using the high collimation and brilliance of the synchrotron beam which allows the usage of slits as small as 0.5 mm in width to select adequate homogeneous parts of both foils, that were 40 cm apart. The small size of the slits ensured that, after the 180° rotation of the sample holder, the same part of the foils was illuminated. The agreement of the experimental spectrum with that of the magnitude reciprocal counterpart setting - seen in the top panel of Figure 2 - justifies our confidence that the reciprocal situation was achieved to a high accuracy. We can see that the scatterer S1 results in reciprocity in the measured intensities, while scatterer S2 exhibits apparent non-reciprocity. The latter outcome is remarkable because of the large non-reciprocal effect: The ratio of intensities of direct and reciprocal scattering is almost 1000 in certain time intervals.

Figure 2. a) Measured and simulated NFS of synchrotron radiation time spectra (count vs. time diagrams, dotted and solid lines, resp.) on scatterer S1 using Si(840) channel cut sigma-analyser (red colour). Results for the reciprocal (source-detector exchanged) situation realised by the 180° rotation of the sample holder (blue colour). The red and blue curves differ in the normalisation only, because of the different duration of the two experiments. b) The analogous experiment using scatterer S2. Almost three orders of magnitude nonreciprocity in certain time intervals was found.

In summary, we have realised a (magnitude) reciprocal and a non-reciprocal experimental arrangement of magnetised α-57Fe foils, which had neither time reversal invariance nor 180° rotational symmetry. Using nuclear resonant scattering of synchrotron radiation, depending on the easily adjustable experimental geometry, reciprocity, and also non-reciprocity over three orders of magnitude, was observed experimentally in intensities that were in full agreement with the theoretical expectations [2]. The presence of the magneto-optic Faraday effect does not automatically lead to non-reciprocity. Further applications in the field of gamma-optics are expected, as non-reciprocal devices belong to an important class of optical components.

Principal publication and authors
Switching reciprocity on and off in a magneto-optical X-ray scattering experiment using nuclear resonance of α-57Fe foils, L. Deák (a), L. Bottyán (a), T. Fülöp (a), G. Kertész (a), D.L. Nagy (a), R. Rüffer (b), H. Spiering (c), F. Tanczikó (a), and G. Vankó (a), Phys. Rev. Lett. 109, 237402 (2012).
(a) Wigner Research Centre for Physics, Budapest (Hungary)
(b) ESRF
(d) Johannes Gutenberg Universität, Mainz (Germany)

References
[1] R.J. Potton, Rep. Prog. Phys 67, 717 (2004).
[2] L. Deák and T. Fülöp, Ann. Phys. (Amsterdam) 327, 1050 (2012).
[3] H. Spiering et al., Hyp. Int. 125, 197 (2000).

Top image: Reciprocity in scattering experiments: the observed signal should not change when reversing the position of source and detector.