Breakdown of the continuum elasticity theory in glasses on the nanometric length-scale

The thermal properties of insulating crystals at low-temperature are governed by low-frequency acoustic excitations. These can be interpreted using a simple continuum elasticity theory – the Debye model – and are characterised by a linear dispersion relation: their characteristic frequency is proportional to the wavenumber, the proportionality constant being the sound velocity. Glasses display a set of universal low-temperature properties that are anomalous with respect to those found in the corresponding crystals [1]. In particular, at a temperature of ~10 K the thermal conductivity shows a plateau and the specific heat is characterised by an excess over the level predicted by the Debye model. This excess is related to the so-called boson peak, an excess of vibrations in the THz frequency range with respect to the Debye model prediction. The physical origin of these universal properties has been lively discussed in the literature for many decades; however, a generally accepted solution is still lacking.

One of the main reasons for this longstanding debate lies in the experimental difficulties of studying the acoustic excitations in disordered systems in the THz and sub-THz frequency range. As a consequence, the experimental data available in the literature are scarce and often even conflicting. The recent advent of the inelastic X-ray scattering (IXS) technique has opened access to the wave-number (q) and frequency (ν) dependence of the longitudinal acoustic excitations with frequencies in the THz range [2]. However, the IXS experiments are currently limited to q ≤ 1 nm^-1 with an instrumental resolution of ~0.3 THz: the (q, ν) region crucial for studying the boson peak remains then close to the edge of the capabilities of the technique. Early IXS results [2] suggested that the longitudinal acoustic excitations in glasses are unaffected across the frequency range where the boson peak appears. More recent results [3] have clarified that they actually experience a regime of strong scattering where their lifetime very quickly decreases on increasing frequency. This regime is below the boson peak frequency position. Further development of the IXS technique has permitted us to collect data of unprecedented quality that sheds new light on the high frequency dynamics of glasses.

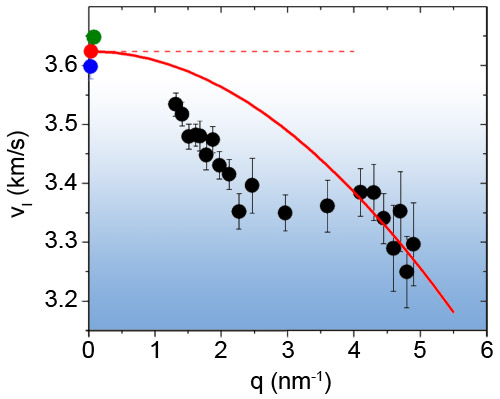
The IXS experiment was carried out at beamline ID16 using the Si(12,12,12) Bragg reflection in backscattering geometry both to monochromatise the incoming X-ray beam (the frequency band width was 0.2 THz) and to frequency-analyse the scattered radiation, thus achieving a total instrumental resolution of 0.3 THz. IXS spectra were collected for q values between 1.5 and 5 nm^-1. Just like for simple crystals, the frequency position of the maximum of the inelastic scattering spectrum divided by q gives a sound velocity. The main result of the present study is that this velocity is characterised by an unexpected, marked decrease with respect to the macroscopic value at q-values of a few nm^-1, see Figure 1. This corresponds to frequencies of ~1 THz, i.e. exactly to the frequency range where the boson peak appears in this glass. This connection can in fact be made quantitative, and clarifies that the boson peak and the aforementioned universal excess over the Debye model prediction found in the specific heat of glasses at temperatures of ~10 K originate indeed from the peculiar acoustic properties of glasses.

Figure 1. Wavevector dependence of the longitudinal sound velocity of a glass of glycerol at 150.1 K obtained using inelastic X-ray scattering (black circles). These data are compared to literature data measured with lower frequency techniques: stimulated Brillouin gain spectroscopy (blue circle), Brillouin light scattering (red circle), and inelastic ultraviolet scattering (green circle) - see principal publication for references to the original papers. The dashed line indicates the macroscopic sound limit, while the full line corresponds to a simple sinusoidal, crystal-like description for the deviation of the sound velocity from the macroscopic limit. The marked decrease of the sound velocity in the glass at q~2 nm-1 shows that on the corresponding length-scale the continuum elasticity theory no longer holds.

In other words, in crystals the continuum elasticity model holds true on a length-scale much larger than the interatomic spacing and gradually breaks down when approaching the microscopic scale. Whereas in glasses, the structural disorder undermines the continuum Debye model in a more drastic way: the continuum elasticity theory breaks down abruptly on the mesoscopic length-scale of about ten interatomic spacings characteristic of the medium range order, where it still works well for the corresponding crystalline systems.

References
[1] W.A. Phillips, Amorphous Solids: Low Temperature Properties (Springer, Berlin, 1981).
[2] F. Sette, M. Krisch, C. Masciovecchio, G. Ruocco, and G. Monaco, Science 280, 1550 (1998).
[3] B. Rufflé, G. Guimbrètiere, E. Courtens, R. Vacher, and G. Monaco, Phys. Rev. Lett. 96, 045502 (2006).

Principal publication and authors
G. Monaco, V.M. Giordano, Breakdown of the Debye approximation for the acoustic modes with nanometric wavelengths in glasses, Proc. Natl. Acad. Sci. USA 106, 3659 (2009).
ESRF