Studying atomic dynamics with coherent X-rays

Diffusion in solids is conventionally studied by the radiotracer technique. This is a macroscopic technique, i.e. it is sensitive only to atomic displacements composed of many atomic jumps, and therefore only the diffusion constant can be measured. Microscopic techniques, however, aim at characterising atomic dynamics by the frequency, length and direction of the elementary atomic jump. X-ray photon correlation spectroscopy (XPCS) has potential as a universal microscopic technique, i.e. it is not bound to certain isotopes or elements. In XPCS, coherent X-rays are scattered by the sample and the temporal variation of the scattered intensity – the so-called speckle pattern – is recorded as a function of the wave vector q.

In this study we performed the first successful XPCS measurement of atomic dynamics. Experiments were carried out at beamline ID10A. The sample was a single crystal of Cu₉₀Au₁₀ at temperatures around 540 K, where it forms a disordered solid solution, albeit with a certain degree of short-range order. Time series of the scattered intensity I(q,t) at a given q and time t were recorded with a CCD detector and evaluated via the standard intensity-intensity auto-correlation function:

  ,

 where the average is taken over the absolute time t and the pixels of the detector. The decay of the auto-correlation function was fit to an exponential offset by 1 with a q-dependent correlation time τ(q) (see Figure 1).

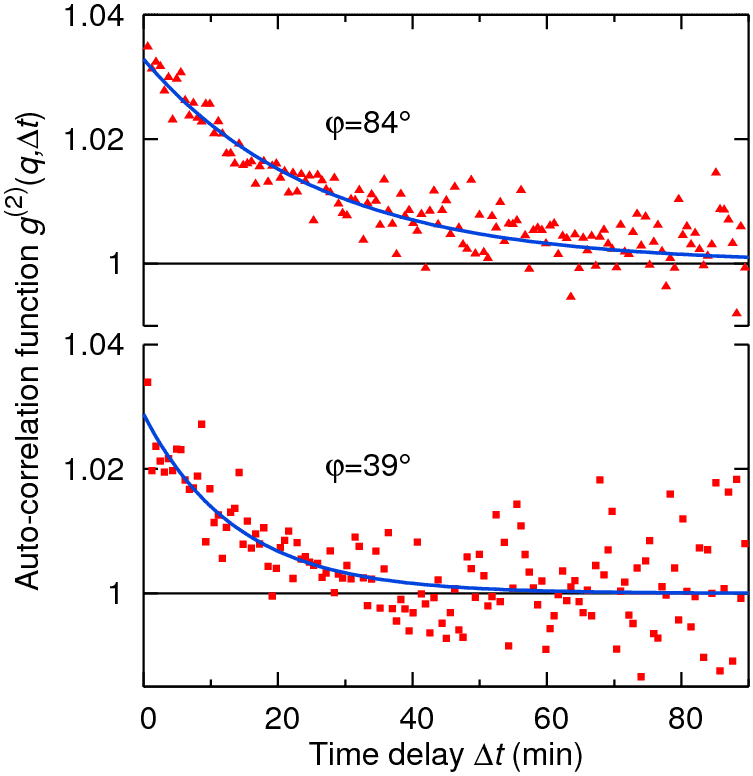Figure 1. Auto-correlation functions for two orientations, both with a scattering angle of 2θ = 25°.

As the sample was a single crystal, rotating the detector around the direction of the incident beam for a fixed scattering angle 2θ (corresponding to same length, but different orientation of q) leads to variations of the fitted correlation time due to the discrete and directed nature of the atomic jumps. Apart from this variation due to the jump geometry, short-range order also influences the correlation time, a fact which is well known as de Gennes-narrowing from XPCS measurements in liquids [1]. Figure 2 shows the correlation time as a function of the azimuthal angle together with fits taking into account de Gennes-narrowing with the quantitative theory from ref. [2]. The results clearly demonstrate that diffusion happens via nearest-neighbour exchanges.

Figure 2. Correlation times as a function of azimuthal angle φ for a scattering angle of 2θ = 25° (corresponding to |q|=1.75 Å-1) at 543 K together with fits assuming nearest-neighbour (blue) and second-nearest-neighbour exchanges (green).

The fitted residence time, i.e. the average time between jumps for a given atom, is 2200 seconds at 543 K. By varying the temperature, the activation enthalpy was determined to be 2.1 eV. These results establish XPCS as a complementary method to those working in the energy domain such as quasi-elastic neutron scattering, which are restricted to jump frequencies in the MHz range. It should be possible to explore the gap between these timescales once hard X-ray free-electron lasers with their dramatically increased intensity are available.

References
[1] C. Caronna, Y. Chushkin, A. Madsen, A. Cupane, Phys. Rev. Lett. 100, 055702 (2008).
[2] S.K. Sinha, D.K. Ross, Physica B 149, 51 (1988).

Principal publication and authors
M. Leitner (a), B. Sepiol (a), L.-M. Stadler (b), B. Pfau (c) and G. Vogl (a), Atomic diffusion studied with coherent X-rays, Nature Materials 8, 717-720 (2009).
(a) Fakultät für Physik, Universität Wien (Austria)
(b) HASYLAB at DESY, Hamburg (Germany)
(c) Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Berlin (Germany)