- Home
- Users & Science
- Find a beamline
- Collaborating research group beamlines
- BM20 - ROBL - The Rossendorf Beamline
- Software
- Wavelet Transform for EXAFS
Wavelet Transform for EXAFS
EXAFS analysis is based on the backscattering of electron waves from atomic neighbors surrounding a central atom, which is excited by an x-ray photon of the appropriate energy. The interference between the outgoing electron wave and the backscattered electron waves creates an interference pattern, which is subsequently analyzed to derive nature, number, and distance (plus disorder) of the neighboring atoms.
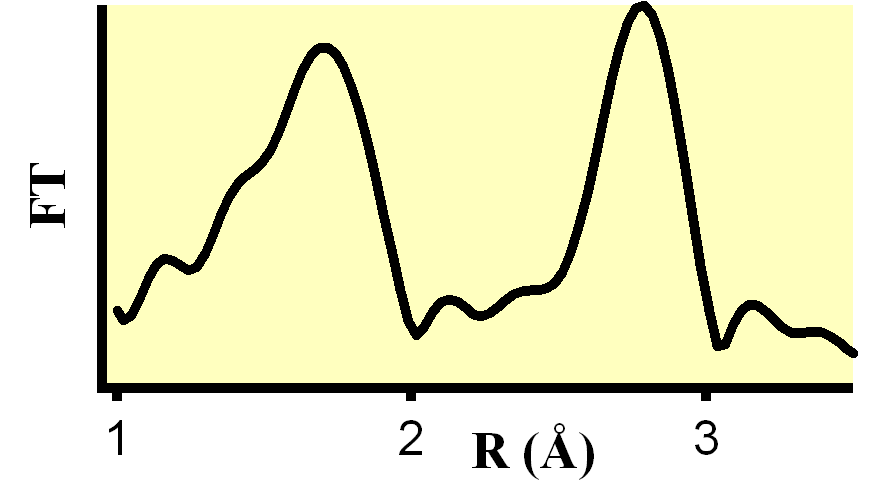
One of the most fundamental steps during the analysis is the Fourier transform, which separates the neighboring atoms according to their distances from the central atom (see left figure). The nature of the neighboring atoms is identified by the k-space dependence of the wave function after a Fourier backtransform of an atom shell, i.e. of all the atoms at a specific distance. Often such shells consist of only one type of atoms (e.g. oxygen atom in the first coordination sphere of oxides). If such a shell comprises atoms of different elements, however, their waves cannot be separated by the Fourier transform/backtransform approach. While one might identify these atoms simply by trial-and-error fits, the wavelet transform fills in just the gap left by the Fourier transform: The Wavelet transform resolves the centers of the backscattering wave functions in energy (or wave vector) space, therefore offers a straight-forward way to discriminate different atoms within one atomic shell.
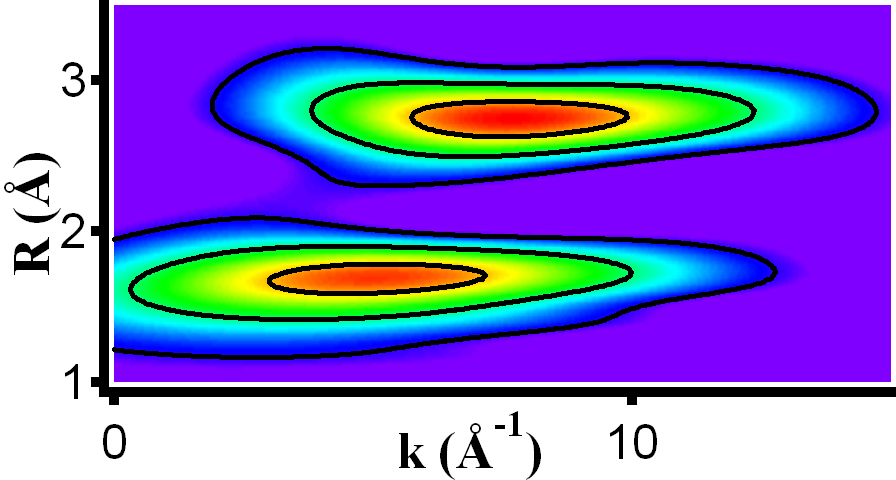
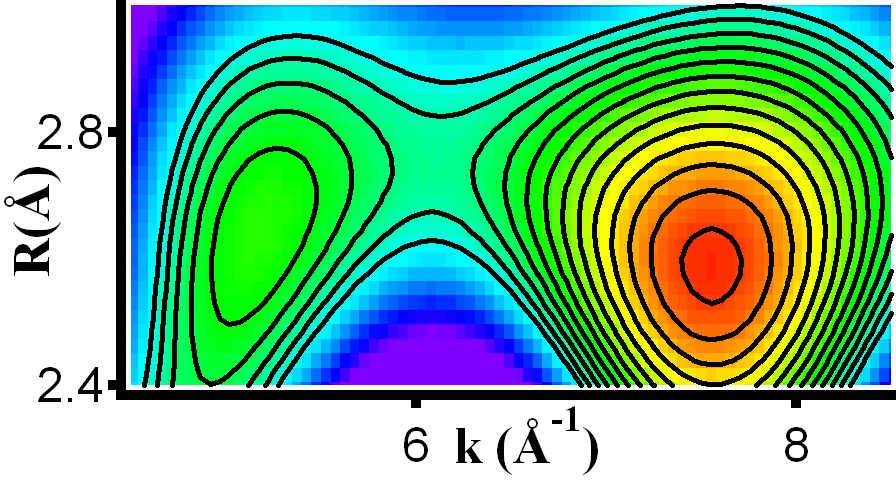
As one can see in the figure below, the Wavelet overview (center) reveals the distance information along the y-axis quite similar to the Fourier transform shown left, but in addition also their energy dependence along the x-axis. While the wavelet overview shows only two types of atoms at two distances, the detail figure (right) resolves two types of atoms in the more distance shell (R~2.6 Å).
 |
 |
 |
|
Fourier transform magnitude |
Wavelet overview |
Wavelet detail |
Software (Manuals & Downloads)
A suite of software modules for the calculation and graphical output of EXAFS Wavelet analysis has been developed by Marina Chukalina (IMT-RAS) and Harald Funke (IRC-FZR):
| Fortran | platform free |
| IGOR Pro | Windows |
| Python | Windows |
References
Useful Links
|
|
|



